题目内容
已知等差数列{an}的前n项和为Sn,并且a2=2,S5=15,数列{bn}满足:b1=
,bn+1=
bn(n∈N+),记数列{bn}的前n项和为Tn.
(1)求数列{an}的通项公式an及前n项和公式Sn;
(2)求数列{bn}的通项公式bn及前n项和公式Tn;
(3)记集合M={n|
≥λ,n∈N+},若M的子集个数为16,求实数λ的取值范围.
| 1 |
| 2 |
| n+1 |
| 2n |
(1)求数列{an}的通项公式an及前n项和公式Sn;
(2)求数列{bn}的通项公式bn及前n项和公式Tn;
(3)记集合M={n|
| 2Sn(2-Tn) |
| n+2 |
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:(1)利用等差数列的通项公式和前n项和公式即可得出;
(2)先得到
=
•
,再利用累乘法,得到数列{bn}的通项公式,再利用错位相减法求出前n项和公式Tn;
(3)根据函数的f(n)=
的单调性,得到不等式
≥λ,n∈N+继而求实数λ的取值范围
(2)先得到
| bn+1 |
| bn |
| 1 |
| 2 |
| n+1 |
| n |
(3)根据函数的f(n)=
| n2+n |
| 2n |
| n2+n |
| 2n |
解答:
解:(1)设数列{an}的公差为d,
由题意得
,解得
,
∴an=n,
∴Sn=
.
(2)由题意得
=
•
,
累乘得bn=
•
•…•
•b1=(
)n(
×
×…×
)=
.
由题意得Tn=
+
+
+…+
①
Tn=
+
+
+…+
+
②
②-①得:
Tn=
+
+
+…+
-
=
-
=1--
∴Tn=2-
(3)由上面可得
=
,令f(n)=
,
则f(1)=1,f(2)=
,f(3)=
,f(4)=
,f(5)=
.
下面研究数列f(n)=
的单调性,
∵f(n+1)-f(n)=
-
=
,
∴n≥3时,f(n+1)-f(n)<0,f(n+1)<f(n),即f(n)单调递减.
∵集合M的子集个数为16,
∴M中的元素个数为4,
∴不等式
≥λ,n∈N+解的个数为4,
∴
<λ≤1
由题意得
|
|
∴an=n,
∴Sn=
| n2+n |
| 2 |
(2)由题意得
| bn+1 |
| bn |
| 1 |
| 2 |
| n+1 |
| n |
累乘得bn=
| bn |
| bn-1 |
| bn-1 |
| bn-2 |
| b2 |
| b1 |
| 1 |
| 2 |
| n |
| n-1 |
| n-1 |
| n-2 |
| 2 |
| 1 |
| n |
| 2n |
由题意得Tn=
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 2 |
| 23 |
| 3 |
| 24 |
| n-1 |
| 2n |
| n |
| 2n+1 |
②-①得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| n |
| 2n+1 |
| ||||
1-
|
| n |
| 2n+1 |
| n+2 |
| 2n+1 |
∴Tn=2-
| n+2 |
| 2n |
(3)由上面可得
| 2Sn(2-Tn) |
| n+2 |
| n2+n |
| 2n |
| n2+n |
| 2n |
则f(1)=1,f(2)=
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
| 15 |
| 16 |
下面研究数列f(n)=
| n2+n |
| 2n |
∵f(n+1)-f(n)=
| (n+1)2+n+1 |
| 2n+1 |
| n2+n |
| 2n |
| (n+1)(2-n) |
| 2n+1 |
∴n≥3时,f(n+1)-f(n)<0,f(n+1)<f(n),即f(n)单调递减.
∵集合M的子集个数为16,
∴M中的元素个数为4,
∴不等式
| n2+n |
| 2n |
∴
| 15 |
| 16 |
点评:本题考查了等差数列的通项公式和前n项和公式、累乘法错位相减法求和,以及参数的取值范围,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
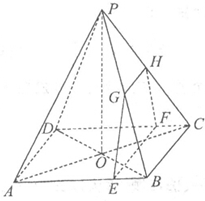 如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2
如图,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2