题目内容
5.一个四棱锥的三视图如图所示,则该四棱锥外接球的体积为$4\sqrt{3}π$.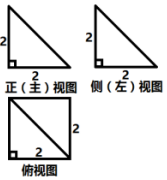
分析 根据三视图知几何体是四棱锥为棱长为2的正方体一部分,画出直观图,由正方体的性质求出外接球的半径,由球的体积公式求出即可.
解答 解:根据三视图知几何体是: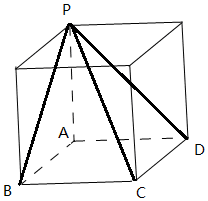
四棱锥P-ABCD是棱长为2正方体一部分,
直观图如图所示:
则四棱锥P-ABCD的外接球是此正方体的外接球,
设外接球的半径是R,
由正方体的性质可得,2R=$\sqrt{{2}^{2}+{2}^{2}+{2}^{2}}$,解得R=$\sqrt{3}$,
所以该棱锥的外接球的体积V=$\frac{4}{3}π×{R}^{3}$=$4\sqrt{3}π$,
故答案为:$4\sqrt{3}π$.
点评 本题考查由三视图求几何体外接球的体积,在三视图与直观图转化过程中,以一个正方体为载体是很好的方式,使得作图更直观,考查空间想象能力.

练习册系列答案
相关题目
20.已知某几何体的三视图如图,则该几何体的表面积是( )
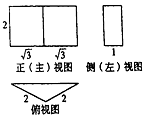

| A. | $4+4\sqrt{3}$ | B. | $4+6\sqrt{3}$ | C. | $8+6\sqrt{3}$ | D. | $8+8\sqrt{3}$ |
15.命题“?x∈[1,2],x2-3x+2≤0”的否定是( )
| A. | ?x∈[1,2],x2-3x+2>0 | B. | ?x∉[1,2],x2-3x+2>0 | ||
| C. | $?{x_0}∈[{1,2}],{x_0}^2-3{x_0}+2>0$ | D. | $?{x_0}∉[{1,2}],{x_0}^2-3{x_0}+2>0$ |