题目内容
15.命题“?x∈[1,2],x2-3x+2≤0”的否定是( )| A. | ?x∈[1,2],x2-3x+2>0 | B. | ?x∉[1,2],x2-3x+2>0 | ||
| C. | $?{x_0}∈[{1,2}],{x_0}^2-3{x_0}+2>0$ | D. | $?{x_0}∉[{1,2}],{x_0}^2-3{x_0}+2>0$ |
分析 根据已知中的原命题,结合全称命题否定的方法,可得答案.
解答 解:命题:“?x∈[1,2],x2-3x+2≤0的否定是$?{x_0}∈[{1,2}],{x_0}^2-3{x_0}+2>0$,
故选:C
点评 本题考查的知识点是全称命题,命题的否定,难度不大,属于基础题.

练习册系列答案
相关题目
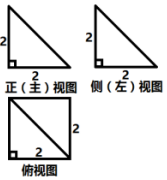
6.如图为某几何体的三视图,则该几何体的外接球的直径为( )

| A. | 10 | B. | $\sqrt{34}$ | C. | 5 | D. | $\frac{{\sqrt{34}}}{2}$ |
20.已知等差数列{an}满足:a2=2,Sn-Sn-3=54(n>3),Sn=100,则n=( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
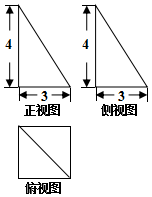
7.某几何体的三视图如图所示,在该几何体的体积是( )

| A. | $\frac{10}{3}$ | B. | $\frac{20}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
4.以双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上一点M为圆心作圆,该圆与x轴相切于C的一个焦点F,与y轴交于P,Q两点,若△MPQ为正三角形,则C的离心率等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
5.已知复数$z=\frac{a+i}{1-i}$(其中i为虚数单位),若z为纯虚数,则实数a等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | $\sqrt{2}$ |