题目内容
10．某几何体的三视图如图所示，则该几何体的体积为$\frac{4}{3}$．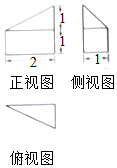
分析 根据几何体的三视图知，该几何体是直三棱柱与三棱锥的组合体；
结合图中数据，计算它的体积即可．
解答 解：根据几何体的三视图知，
该几何体是下部为直三棱柱，上部为三棱锥的组合体；
且组合体的底面为直角三角形，
根据图中数据，计算组合体的体积为
V组合体=V三棱柱+V三棱锥
=$\frac{1}{2}$×2×1×1+$\frac{1}{3}$×$\frac{1}{2}$×2×1×1
=$\frac{4}{3}$．
故答案为：$\frac{4}{3}$．
点评 本题考查了空间几何体三视图的应用问题，是基础题目．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
20．
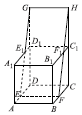如图所示，在棱长为a的正方体ABCD-A1B2C3D4中，点E，F分别在棱AD，BC上，且AE=BF=$\frac{1}{3}$a．过EF的平面绕EF旋转，与DD1、CC1的延长线分别交于G，H点，与A1D1、B1C1分别交于E1，F1点．当异面直线FF1与DD1所成的角的正切值为$\frac{1}{3}$时，|GF1|=（ ）
如图所示，在棱长为a的正方体ABCD-A1B2C3D4中，点E，F分别在棱AD，BC上，且AE=BF=$\frac{1}{3}$a．过EF的平面绕EF旋转，与DD1、CC1的延长线分别交于G，H点，与A1D1、B1C1分别交于E1，F1点．当异面直线FF1与DD1所成的角的正切值为$\frac{1}{3}$时，|GF1|=（ ）| A． | $\frac{\sqrt{19}a}{3}$ | B． | $\frac{\sqrt{19}a}{9}$ | C． | $\frac{\sqrt{2}a}{3}$ | D． | $\frac{\sqrt{2}a}{9}$ |
15．命题“对任意的x∈R，x3-x+1≤0”的否定是（ ）
| A． | 不存在x∈R，x3-x+1≤0 | B． | 存在x∈R，x3-x+1≤0 | ||
| C． | 对任意的x∈R，x3-x+1＞0 | D． | 存在x∈R，x3-x+1＞0 |
2．
如图，正方体ABCD-A1B1C1D1的棱长为1，点M∈AB1，N∈BC1，且AM=BN≠$\sqrt{2}$，有以下四个结论：①AA1⊥MN；②AB∥MN；③MN∥平面A1B1C1D1；④MN与A1C1一定是异面直线．其中正确命题的序号是（ ）
如图，正方体ABCD-A1B1C1D1的棱长为1，点M∈AB1，N∈BC1，且AM=BN≠$\sqrt{2}$，有以下四个结论：①AA1⊥MN；②AB∥MN；③MN∥平面A1B1C1D1；④MN与A1C1一定是异面直线．其中正确命题的序号是（ ）| A． | ①③ | B． | ②③ | C． | ①④ | D． | ①③④ |
19．
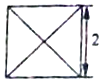已知某几何体的俯视图是如图所示的边长为2的正方形，主视图与左视图是边长为2的正三角形，则其侧面积（ ）
已知某几何体的俯视图是如图所示的边长为2的正方形，主视图与左视图是边长为2的正三角形，则其侧面积（ ）| A． | 4 | B． | $4\sqrt{3}$ | C． | $4（1+\sqrt{3}）$ | D． | 8 |
20．已知等差数列{an}满足：a2=2，Sn-Sn-3=54（n＞3），Sn=100，则n=（ ）
| A． | 7 | B． | 8 | C． | 9 | D． | 10 |