题目内容
14.三棱锥P-ABC中,侧棱PA=2,PB=PC=$\sqrt{6}$,则当三棱锥P-ABC的三个侧面的面积和最大时,经过点P,A,B,C的球的表面积是( )| A. | 4π | B. | 8π | C. | 12π | D. | 16π |
分析 三棱锥P-ABC的三条侧棱PA、PB、PC两两互相垂直,三棱锥P-ABC的三个侧面的面积之和最大,它的外接球就是它扩展为长方体的外接球,求出长方体的对角线的长,就是球的直径,然后求球的表面积.
解答 解:当PA,PB,PC两两垂直时,三棱锥P-ABC的三个侧面的面积和最大,
此时2R=$\sqrt{6+6+4}$=4,S=4π•4=16π,
故选D.
点评 本题考查球的表面积,几何体的外接球,考查空间想象能力,计算能力,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2. 如图,正方体ABCD-A1B1C1D1的棱长为1,点M∈AB1,N∈BC1,且AM=BN≠$\sqrt{2}$,有以下四个结论:①AA1⊥MN;②AB∥MN;③MN∥平面A1B1C1D1;④MN与A1C1一定是异面直线.其中正确命题的序号是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,点M∈AB1,N∈BC1,且AM=BN≠$\sqrt{2}$,有以下四个结论:①AA1⊥MN;②AB∥MN;③MN∥平面A1B1C1D1;④MN与A1C1一定是异面直线.其中正确命题的序号是( )
 如图,正方体ABCD-A1B1C1D1的棱长为1,点M∈AB1,N∈BC1,且AM=BN≠$\sqrt{2}$,有以下四个结论:①AA1⊥MN;②AB∥MN;③MN∥平面A1B1C1D1;④MN与A1C1一定是异面直线.其中正确命题的序号是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,点M∈AB1,N∈BC1,且AM=BN≠$\sqrt{2}$,有以下四个结论:①AA1⊥MN;②AB∥MN;③MN∥平面A1B1C1D1;④MN与A1C1一定是异面直线.其中正确命题的序号是( )| A. | ①③ | B. | ②③ | C. | ①④ | D. | ①③④ |
19.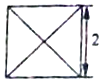 已知某几何体的俯视图是如图所示的边长为2的正方形,主视图与左视图是边长为2的正三角形,则其侧面积( )
已知某几何体的俯视图是如图所示的边长为2的正方形,主视图与左视图是边长为2的正三角形,则其侧面积( )
 已知某几何体的俯视图是如图所示的边长为2的正方形,主视图与左视图是边长为2的正三角形,则其侧面积( )
已知某几何体的俯视图是如图所示的边长为2的正方形,主视图与左视图是边长为2的正三角形,则其侧面积( )| A. | 4 | B. | $4\sqrt{3}$ | C. | $4(1+\sqrt{3})$ | D. | 8 |
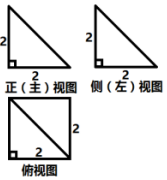
6.如图为某几何体的三视图,则该几何体的外接球的直径为( )
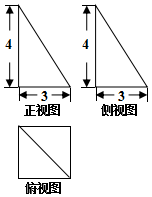

| A. | 10 | B. | $\sqrt{34}$ | C. | 5 | D. | $\frac{{\sqrt{34}}}{2}$ |
4.以双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上一点M为圆心作圆,该圆与x轴相切于C的一个焦点F,与y轴交于P,Q两点,若△MPQ为正三角形,则C的离心率等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
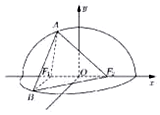 已知椭圆Γ的左、右焦点分别为F1(-1,0)、F2(1,0).经过点F1且倾斜角为θ(0<θ<π)的直线l与椭圆Γ交于A、B两点(其中点A在x轴上方),△ABF2的周长为8.
已知椭圆Γ的左、右焦点分别为F1(-1,0)、F2(1,0).经过点F1且倾斜角为θ(0<θ<π)的直线l与椭圆Γ交于A、B两点(其中点A在x轴上方),△ABF2的周长为8.