题目内容
已知f(x)是定义在R上且周期为3的函数,当x∈[0,3)时,f(x)=|x2-2x+
|,若函数y=f(x)-a在区间[-3,4]上有10个零点(互不相同),则实数a的取值范围是 .
| 1 |
| 2 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:在同一坐标系中画出函数的图象与直线y=a的图象,利用数形结合判断a的范围即可.
解答:
 解:f(x)是定义在R上且周期为3的函数,当x∈[0,3)时,f(x)=|x2-2x+
解:f(x)是定义在R上且周期为3的函数,当x∈[0,3)时,f(x)=|x2-2x+
|,若函数y=f(x)-a在区间[-3,4]上有10个零点(互不相同),在同一坐标系中画出函数f(x)与y=a的图象如图:由图象可知a∈(0,
).
故答案为:(0,
).
 解:f(x)是定义在R上且周期为3的函数,当x∈[0,3)时,f(x)=|x2-2x+
解:f(x)是定义在R上且周期为3的函数,当x∈[0,3)时,f(x)=|x2-2x+| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(0,
| 1 |
| 2 |
点评:本题考查函数的图象以函数的零点的求法,数形结合的应用.

练习册系列答案
相关题目
将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是( )
| A、4π | B、3π | C、2π | D、π |
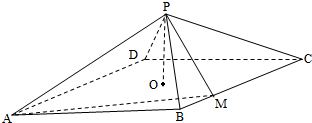 如图,四棱锥P-ABCD,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=
如图,四棱锥P-ABCD,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=