题目内容
在平面直角坐标系xOy中,若曲线y=ax2+
(a,b为常数)过点P(2,-5),且该曲线在点P处的切线与直线7x+2y+3=0平行,则a+b的值是 .
| b |
| x |
考点:利用导数研究曲线上某点切线方程
专题:导数的概念及应用
分析:由曲线y=ax2+
(a,b为常数)过点P(2,-5),且该曲线在点P处的切线与直线7x+2y+3=0平行,可得y|x=2=-5,且y′|x=2=-
,解方程可得答案.
| b |
| x |
| 7 |
| 2 |
解答:
解:∵直线7x+2y+3=0的斜率k=-
,
曲线y=ax2+
(a,b为常数)过点P(2,-5),且该曲线在点P处的切线与直线7x+2y+3=0平行,
∴y′=2ax-
,
∴
,
解得:
,
故a+b=-3,
故答案为:-3
| 7 |
| 2 |
曲线y=ax2+
| b |
| x |
∴y′=2ax-
| b |
| x2 |
∴
|
解得:
|
故a+b=-3,
故答案为:-3
点评:本题考查的知识点是利用导数研究曲线上某点切线方程,其中根据已知得到y|x=2=-5,且y′|x=2=-
,是解答的关键.
| 7 |
| 2 |

练习册系列答案
相关题目
已知Rt△ABC中,AB=8,AC=4,BC=4
,则对于△ABC所在平面内的一点P,
•(
+
)的最小值是( )
| 3 |
| PA |
| PB |
| PC |
| A、-14 | B、-8 |
| C、-26 | D、-30 |
 一同学为研究函数f(x)=
一同学为研究函数f(x)=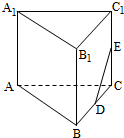 在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形
在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形