题目内容
已知圆O:x2+y2=1和点A(-2,0),若定点B(b,0)(b≠-2)和常数λ满足:对圆O上任意一点M,都有|MB|=λ|MA|,则:
(Ⅰ)b= ;
(Ⅱ)λ= .
(Ⅰ)b=
(Ⅱ)λ=
考点:三点共线
专题:直线与圆
分析:(Ⅰ)利用|MB|=λ|MA|,可得(x-b)2+y2=λ2(x+2)2+λ2y2,由题意,取(1,0)、(-1,0)分别代入,即可求得b;
(Ⅱ)取(1,0)、(-1,0)分别代入,即可求得λ.
(Ⅱ)取(1,0)、(-1,0)分别代入,即可求得λ.
解答:
解:解法一:设点M(cosθ,sinθ),则由|MB|=λ|MA|得(cosθ-b)2+sin2θ=λ2[(cosθ+2)2+sin2θ],即
-2bcosθ+b2+1=4λ2cosθ+5γ2对任意θ都成立,所以
.又由|MB|=λ|MA|得λ>0,且b≠-2,解得
.
解法二:(Ⅰ)设M(x,y),则
∵|MB|=λ|MA|,
∴(x-b)2+y2=λ2(x+2)2+λ2y2,
由题意,取(1,0)、(-1,0)分别代入可得(1-b)2=λ2(1+2)2,(-1-b)2=λ2(-1+2)2,
∴b=-
,λ=
.
(Ⅱ)由(Ⅰ)知λ=
.
故答案为:-
,
.
-2bcosθ+b2+1=4λ2cosθ+5γ2对任意θ都成立,所以
|
|
解法二:(Ⅰ)设M(x,y),则
∵|MB|=λ|MA|,
∴(x-b)2+y2=λ2(x+2)2+λ2y2,
由题意,取(1,0)、(-1,0)分别代入可得(1-b)2=λ2(1+2)2,(-1-b)2=λ2(-1+2)2,
∴b=-
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)由(Ⅰ)知λ=
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查圆的方程,考查赋值法的运用,考查学生的计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为
,D为BC中点,则三棱锥A-B1DC1的体积为( )
| 3 |
| A、3 | ||||
B、
| ||||
| C、1 | ||||
D、
|
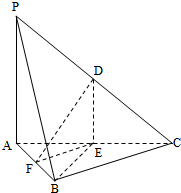 如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证:
如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证: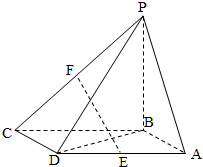 如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=
如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD= 从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图: