题目内容
将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是( )
| A、4π | B、3π | C、2π | D、π |
考点:旋转体(圆柱、圆锥、圆台)
专题:计算题,空间位置关系与距离
分析:边长为1的正方形,绕其一边所在直线旋转一周,得到的几何体为圆柱,从而可求圆柱的侧面积.
解答:
解:边长为1的正方形,绕其一边所在直线旋转一周,得到的几何体为圆柱,
则所得几何体的侧面积为:1×2π×1=2π,
故选:C.
则所得几何体的侧面积为:1×2π×1=2π,
故选:C.
点评:本题是基础题,考查旋转体的侧面积的求法,考查计算能力.

练习册系列答案
相关题目
已知Rt△ABC中,AB=8,AC=4,BC=4
,则对于△ABC所在平面内的一点P,
•(
+
)的最小值是( )
| 3 |
| PA |
| PB |
| PC |
| A、-14 | B、-8 |
| C、-26 | D、-30 |
正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为
,D为BC中点,则三棱锥A-B1DC1的体积为( )
| 3 |
| A、3 | ||||
B、
| ||||
| C、1 | ||||
D、
|
设U=R,P={x|x<1},Q={x|x2≥4},则P∩∁UQ=( )
| A、{x|-1<x<2} |
| B、{x|-2<x<1} |
| C、{x|1<x<2} |
| D、{x|-2<x<2} |
已知a,b是正数,且a+b=1,则
+
( )
| 1 |
| a |
| 4 |
| b |
| A、有最小值8 |
| B、有最小值9 |
| C、有最大值8 |
| D、有最大值9 |
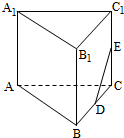 在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形
在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形