题目内容
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.(1)证明CD⊥AE;
(2)证明PD⊥平面ABE;
(3)求二面角A-PD-C的正切值.
考点:二面角的平面角及求法
专题:计算题,证明题,空间位置关系与距离,空间角
分析:(1)运用线面垂直的判定和性质定理即可得证CD⊥AE;
(2)运用线面垂直的性质和判定定理,即可得到PD⊥平面ABE;
(3)过E点作EM⊥PD于M点,连结AM,由(2)知AE⊥平面PCD,则AM⊥PD,则∠AME是二面角A-PD-C的平面角.通过解三角形AEM,即可得到所求值.
(2)运用线面垂直的性质和判定定理,即可得到PD⊥平面ABE;
(3)过E点作EM⊥PD于M点,连结AM,由(2)知AE⊥平面PCD,则AM⊥PD,则∠AME是二面角A-PD-C的平面角.通过解三角形AEM,即可得到所求值.
解答:
 (1)证明:∵PA⊥底面ABCD,CD?平面ABCD,∴PA⊥CD,
(1)证明:∵PA⊥底面ABCD,CD?平面ABCD,∴PA⊥CD,
又AC⊥CD,AC∩PA=A,
∴CD⊥平面PAC,又AE?平面PAC,
∴CD⊥AE;
(2)证明:∵PA⊥底面ABCD,AB?平面ABCD∴PA⊥AB,
又AD⊥AB,AD∩PA=A
∴AB⊥平面PAD,又PD?平面PAD∴AB⊥PD,
由PA=AB=BC,∠ABC=60°,则△ABC是正三角形.
∴AC=AB∴PA=PC
∵E是PC中点∴AE⊥PC
由(1)知AE⊥CD,又CD∩PC=C∴AE⊥平面PCD
∴AE⊥PD,又AB⊥PD,AB∩AE=A
∴PD⊥平面ABE;
(3)解:过E点作EM⊥PD于M点,连结AM,
由(2)知AE⊥平面PCD,则AE⊥PD,
则PD⊥平面AEM,∴AM⊥PD,
则∠AME是二面角A-PD-C的平面角.
设AC=a ,AD=
,AD=
=
,PA=A,PD=
=
a,
AM=
=
=
,
在Rt△AEM中,AE=
a,EM=
=
=
a,
则tan∠AME=
=
=
.
 (1)证明:∵PA⊥底面ABCD,CD?平面ABCD,∴PA⊥CD,
(1)证明:∵PA⊥底面ABCD,CD?平面ABCD,∴PA⊥CD,又AC⊥CD,AC∩PA=A,
∴CD⊥平面PAC,又AE?平面PAC,
∴CD⊥AE;
(2)证明:∵PA⊥底面ABCD,AB?平面ABCD∴PA⊥AB,
又AD⊥AB,AD∩PA=A
∴AB⊥平面PAD,又PD?平面PAD∴AB⊥PD,
由PA=AB=BC,∠ABC=60°,则△ABC是正三角形.
∴AC=AB∴PA=PC
∵E是PC中点∴AE⊥PC
由(1)知AE⊥CD,又CD∩PC=C∴AE⊥平面PCD
∴AE⊥PD,又AB⊥PD,AB∩AE=A
∴PD⊥平面ABE;
(3)解:过E点作EM⊥PD于M点,连结AM,
由(2)知AE⊥平面PCD,则AE⊥PD,
则PD⊥平面AEM,∴AM⊥PD,
则∠AME是二面角A-PD-C的平面角.
设AC=a
 ,AD=
,AD=| a |
| cos30° |
| 2a | ||
|
a2+
|
| ||
| 3 |
AM=
| PA•AD |
| PD |
a•
| ||||
|
| 2a | ||
|
在Rt△AEM中,AE=
| ||
| 2 |
| AM2-AE2 |
|
| ||
| 14 |
则tan∠AME=
| AE |
| EM |
| ||||
|
| 7 |
点评:本题考查线面垂直的性质和判定定理及运用,考查空间二面角的求法,考查运算和推理能力,属于中档题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
函数y=
的值域是( )
| 1 |
| tan2x-2tanx+2 |
| A、(-∞,1] | ||
| B、(0,1] | ||
| C、[1,+∞) | ||
D、[
|
 如图,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1、C1D1上的点(点E 与B1不重合),且EH∥A1D1;过EH的平面与棱BB1、CC1相交,交点分别为F、G.
如图,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1、C1D1上的点(点E 与B1不重合),且EH∥A1D1;过EH的平面与棱BB1、CC1相交,交点分别为F、G.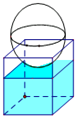 如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为
如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为