题目内容
4.实数m取何值时,复数z=(m2-5m+6)+(m2-3m)i是(1)零;(2)虚数;(3)纯虚数.
分析 (1)由实部等于0,虚部等于0,联立方程组,求解即可得答案;
(2)由虚部不等于0,求解方程即可得答案;
(3)由实部等于0,虚部不等于0,联立方程组,求解即可得答案.
解答 解:(1)复数z=(m2-5m+6)+(m2-3m)i,
当$\left\{\begin{array}{l}{{m}^{2}-5m+6=0}\\{{m}^{2}-3m=0}\end{array}\right.$时,即m=3时,复数z是零;
(2)当m2-3m≠0时,即m≠0且m≠3时,复数z是虚数;
(3)当$\left\{\begin{array}{l}{{m}^{2}-5m+6=0}\\{{m}^{2}-3m≠0}\end{array}\right.$时,即m=2时,复数z是纯虚数.
点评 本题考查了复数的基本概念,是基础题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
14.已知0<α<π,3sin2α=sinα,则cos(α-π)等于( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | -$\frac{1}{6}$ |
19.对a>0,b>0,a+b≥2$\sqrt{ab}$.若x+$\frac{1}{x}$≥2$\sqrt{x•\frac{1}{x}}$,则x+$\frac{1}{x}$≥2,以上推理过程中的错误为( )
| A. | 大前提 | B. | 小前提 | C. | 结论 | D. | 无错误 |
14.已知集合A={x|x2+4≤5x,x∈R},B={y|y>2},则A∩B=( )
| A. | (2,+∞) | B. | (4,+∞) | C. | (2,4] | D. | [2,4] |
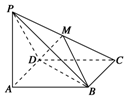 如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,请你补充一个条件①(或③),使平面MBD⊥平面PCD.①DM⊥PC ②DM⊥BM③BM⊥PC ④PM=MC(填写你认为是正确的条件对应的序号).
如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,请你补充一个条件①(或③),使平面MBD⊥平面PCD.①DM⊥PC ②DM⊥BM③BM⊥PC ④PM=MC(填写你认为是正确的条件对应的序号).