题目内容
16.圆(x-1)2+(y-2)2=5被直线x+y+1=0截得的弦长为2$\sqrt{3}$.分析 求出圆心到直线x+y+1=0的距离,再利用勾股定理,即可求得弦长.
解答 解:圆(x-1)2+(y-2)2=5的圆心到直线x+y+1=0的距离为$\frac{|1+2+1|}{\sqrt{2}}$=2$\sqrt{2}$,
∴圆(x-1)2+(y-2)2=5被直线x+y+1=0截得的弦长为2$\sqrt{5-2}$=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查直线与圆 的位置关系,考查点到直线的距离公式,属于中档题.

练习册系列答案
相关题目
8.已知△ABC中,a=1,B=45°,△ABC的面积为2,则三角形外接圆的半径为( )
| A. | $2\sqrt{3}$ | B. | $\frac{{5\sqrt{2}}}{2}$ | C. | $4\sqrt{2}$ | D. | $3\sqrt{2}$ |
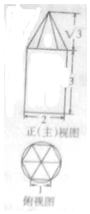 某几何体的正视图与俯视图如图所示,若俯视图中的多边形为正六边形,则该几何体的侧视图的面积为$\frac{15}{2}$.
某几何体的正视图与俯视图如图所示,若俯视图中的多边形为正六边形,则该几何体的侧视图的面积为$\frac{15}{2}$.