题目内容
设集合A为函数y =ln(-x2-2x+8)的定义域,集合B为函数y=x+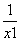 的值域,集合C为不等式(ax-
的值域,集合C为不等式(ax-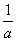 )(x+4)≤0的解集. (1) 求A∩B; (2) 若
)(x+4)≤0的解集. (1) 求A∩B; (2) 若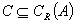 ,求a的取值范围.
,求a的取值范围.
解:(1)由-x2-2x+8>0,解得A=(-4,2),又y=x+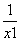 =(x+1)+
=(x+1)+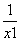 -1,所以B=(-∞,-3]∪ [1,+∞).所以A∩B=(-4,-3]∪[1,2).(2)因为∁RA=(-∞,-4]∪[2,+∞).由
-1,所以B=(-∞,-3]∪ [1,+∞).所以A∩B=(-4,-3]∪[1,2).(2)因为∁RA=(-∞,-4]∪[2,+∞).由 (x+4)≤0,知a≠0.
(x+4)≤0,知a≠0.
①当a>0时,由 (x+4)≤0,得C=
(x+4)≤0,得C= ,不满足C⊆∁RA;
,不满足C⊆∁RA;
②当a<0时,由 (x+4)≥0,得C=(-∞,-4)∪
(x+4)≥0,得C=(-∞,-4)∪ ,欲使C⊆∁RA,则
,欲使C⊆∁RA,则 ≥2,解得-
≥2,解得- ≤a<0或0<a≤
≤a<0或0<a≤ .又a<0,所以-
.又a<0,所以- ≤a<0.综上所述,所求a的取值范围是
≤a<0.综上所述,所求a的取值范围是 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
给出下列三个等式:f(xy)=f(x)+f(y),f(x+y)=f(x)f(y),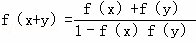 .下列函数中不满足其中任何一个等式的是( )
.下列函数中不满足其中任何一个等式的是( )
|
| A. | f(x)=3x | B. | f(x)=sinx | C. | f(x)=log2x | D. | f(x)=tanx |
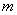 ,
,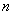 和平面
和平面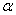 ,
,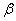 ,若
,若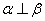 ,
,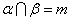 ,
,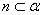 ,
,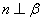 ,则应增加的条件是
,则应增加的条件是 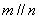 B.
B.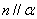 C.
C. 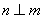 D.
D.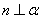
 ,现有四个命题:
,现有四个命题: ,则
,则 ②若
②若
 ④若
④若
 上
上 满足:
满足: ,当
,当 时,
时, ,则
,则 = .
= . 是函数
是函数 的零点,
的零点, ,则①
,则① ;②
;② ;③
;③ ;④
;④ 其中正确的命题是( )(A)①④ (B)②④ (C)①③ (D)②③
其中正确的命题是( )(A)①④ (B)②④ (C)①③ (D)②③ 的反函数
的反函数 ________________.
________________. 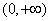 上,函数
上,函数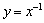 ,
,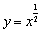 ,
,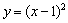 ,
,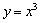 中有三个是增函数;②若
中有三个是增函数;②若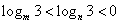 ,则
,则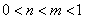 ;③若函数
;③若函数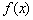 是奇函数,则
是奇函数,则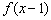 的图象关于点
的图象关于点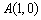 对称;④已知函数
对称;④已知函数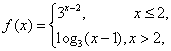 则方程
则方程 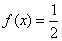 有
有 个实数根,其中正确命题的个数为
个实数根,其中正确命题的个数为  (B)
(B)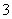 (D)
(D)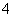
 为偶函数.
为偶函数.  的值;
的值; 有且只有一个根, 求实数
有且只有一个根, 求实数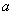 的取值范围.
的取值范围.