题目内容
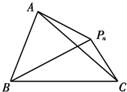如图，△ABC所在平面上的点Pn（n∈N*）均满足△PnAB与△PnAC的面积比为3；1，| PnA |
| xn+1 |
| 3 |
| PnB |
| PnC |
（ ）
| A、65 | B、63 | C、33 | D、31 |
考点：数列递推式,向量的三角形法则
专题：等差数列与等比数列,平面向量及应用
分析：由
=
-（2xn+1）
可得
+（2xn+1）
=
，画出图形后利用三角形面积的关系得到数列递推式，然后构造等比数列得答案．
| PnA |
| xn+1 |
| 3 |
| PnB |
| PnC |
| PnA |
| PnC |
| xn+1 |
| 3 |
| PnB |
解答：
解：由
=
-（2xn+1）
，
得
+（2xn+1）
=
，
设
=(2xn+1)
，
以线段PnA、PnD作出图形如图，
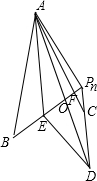
则
+(2xn+1)
=
=
，
∴
=
，∴
=
，
∵
=
=
，∴
=
=
，
则
=
=
，
即xn+1=2xn+1，∴xn+1+1=2（xn+1），
则{xn+1}构成以2为首项，以2为公比的等比数列，
∴x5+1=2•24=32，
则x5=31．
故选：D．
| PnA |
| xn+1 |
| 3 |
| PnB |
| PnC |
得
| PnA |
| PnC |
| xn+1 |
| 3 |
| PnB |
设
| PnD |
| PnC |
以线段PnA、PnD作出图形如图，
则
| PnA |
| PC |
| pnE |
| xn+1 |
| 3 |
| PnB |
∴
|
| ||
|
|
| xn+1 |
| 3 |
| S△PnAE |
| S△PnAB |
| xn+1 |
| 3 |
∵
|
| ||
|
|
| |PnC| |
| |AE| |
| 1 |
| 1+2xn |
| S△PnAC |
| S△PnAD |
| S△PnAC |
| S△PnAE |
| 1 |
| 1+2xn |
则
| S△PnAC |
| S△PnAB |
| xn+1 |
| 3(1+2xn) |
| 1 |
| 3 |
即xn+1=2xn+1，∴xn+1+1=2（xn+1），
则{xn+1}构成以2为首项，以2为公比的等比数列，
∴x5+1=2•24=32，
则x5=31．
故选：D．
点评：本题考查了平面向量的三角形法则，考查了数学转化思想方法，训练了利用构造法构造等比数列，考查了计算能力，属难题．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
若x0是函数f（x）=（
）x-log3x的零点，且0＜x1＜x0，则f（x1）（ ）
| 1 |
| 5 |
| A、恒为正值 | B、等于0 |
| C、恒为负值 | D、不大于0 |
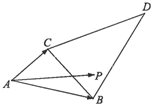
如图，△BCD与△ABC的面积之比为2，点P是区域ABCD内任意一点（含边界），且
=λ
+μ
（λ，μ∈R），则λ+μ的取值范围是（ ）
| AP |
| AB |
| AC |
| A、[0，1] |
| B、[0，2] |
| C、[0，3] |
| D、[0，4] |
函数y=log3x-
的零点大约所在区间为（ ）
| 2 |
| x+1 |
| A、（1，2） |
| B、（2，3） |
| C、（3，4） |
| D、（4，5） |