题目内容
设函数f(x)=ax2+(2b+1)x-a-2(a,b∈R).
(1)若a=0,当x∈[
,1]时恒有f(x)≥0,求b 的取值范围;
(2)若a≠0且b=-1,试在直角坐标平面内找出横坐标不同的两个点,使得函数y=f(x)的图象永远不经过这两点;
(3)若a≠0,函数y=f(x)在区间[3,4]上至少有一个零点,求a2+b2的最小值.
(1)若a=0,当x∈[
| 1 |
| 2 |
(2)若a≠0且b=-1,试在直角坐标平面内找出横坐标不同的两个点,使得函数y=f(x)的图象永远不经过这两点;
(3)若a≠0,函数y=f(x)在区间[3,4]上至少有一个零点,求a2+b2的最小值.
考点:函数的最值及其几何意义,函数的零点与方程根的关系
专题:综合题,函数的性质及应用
分析:(1)求出a=0的解析式,再由一次函数的单调性,得到不等式,即可得到范围;
(2)b=-1时,y=a(x2-1)-x-2,当x2=1时,无论a取任何值,y=-x-2为定值,y=f(x)图象一定过点(1,-3)和(-1,-1),运用函数的定义即可得到结论;
(3)由题意,存在t∈[3,4],使得at2+(2b+1)t-a-2=0,即(t2-1)a+(2t)b+t-2=0,由点到直线的距离意义可知
≥
=
,由此只要求
,t∈[3,4]的最小值.
(2)b=-1时,y=a(x2-1)-x-2,当x2=1时,无论a取任何值,y=-x-2为定值,y=f(x)图象一定过点(1,-3)和(-1,-1),运用函数的定义即可得到结论;
(3)由题意,存在t∈[3,4],使得at2+(2b+1)t-a-2=0,即(t2-1)a+(2t)b+t-2=0,由点到直线的距离意义可知
| a2+b2 |
| |t-2| | ||
|
| |t-2| |
| t2+1 |
| |t-2| |
| t2+1 |
解答:
解:(1)当a=0时,f(x)=(2b+1)x-2,
当x∈[
,1]时恒有f(x)≥0,
则f(
)≥0且f(1)≥0,
即b-
≥0且2b-1≥0,
解得b≥
;
(2)b=-1时,y=a(x2-1)-x-2,
当x2=1时,无论a取任何值,y=-x-2为定值,
y=f(x)图象一定过点(1,-3)和(-1,-1)
由函数定义可知函数图象一定不过A(1,y1)(y1≠-3)和B(-1,y2)(y2≠-1);
(3)由题意,存在t∈[3,4],使得at2+(2b+1)t-a-2=0
即(t2-1)a+(2t)b+t-2=0,
由点到直线的距离意义可知
≥
=
,
由此只要求
,t∈[3,4]的最小值.
令g(t)=
,t∈[3,4]
设u=t-2,u∈[1,2],则
g(t)=f(u)=
=
∴u=1,即t=3时,g(t)取最小值
,
∴t=3时,a2+b2的最小值为
.
当x∈[
| 1 |
| 2 |
则f(
| 1 |
| 2 |
即b-
| 3 |
| 2 |
解得b≥
| 3 |
| 2 |
(2)b=-1时,y=a(x2-1)-x-2,
当x2=1时,无论a取任何值,y=-x-2为定值,
y=f(x)图象一定过点(1,-3)和(-1,-1)
由函数定义可知函数图象一定不过A(1,y1)(y1≠-3)和B(-1,y2)(y2≠-1);
(3)由题意,存在t∈[3,4],使得at2+(2b+1)t-a-2=0
即(t2-1)a+(2t)b+t-2=0,
由点到直线的距离意义可知
| a2+b2 |
| |t-2| | ||
|
| |t-2| |
| t2+1 |
由此只要求
| |t-2| |
| t2+1 |
令g(t)=
| |t-2| |
| t2+1 |
设u=t-2,u∈[1,2],则
g(t)=f(u)=
| u |
| u2+4u+5 |
| 1 | ||
u+
|
∴u=1,即t=3时,g(t)取最小值
| 1 |
| 10 |
∴t=3时,a2+b2的最小值为
| 1 |
| 100 |
点评:本题考查不等式的恒成立问题转化为求函数的值域问题,主要考查一次函数的单调性,运用主元法和直线和圆有交点的条件是解题的关键.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
若复数Z1=1+i,Z2=3-i,则
=( )
| Z2 |
| Z1 |
| A、1+i | B、1+2i |
| C、1-2i | D、2-2i |
设函数f(x)=x3-22-x的零点为x0,则x0所在的大致区间是( )
| A、(3,4) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
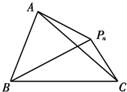 如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3;1,
如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3;1,| PnA |
| xn+1 |
| 3 |
| PnB |
| PnC |
( )
| A、65 | B、63 | C、33 | D、31 |
若函数f(x)=(x-1)(x-3)+(x-3)(x-4)+(x-4)(x-1),则函数f(x)的两个零点分别位于区间( )
| A、(1,3)和(3,4)内 |
| B、(-∞,1)和(1,3)内 |
| C、(3,4)和(4,+∞)内 |
| D、(-∞,1)和(4,+∞)内 |
集合M={x|(
)x≥1},N={x|y=lg(x+2)},则M∩N等于( )
| 1 |
| 2 |
| A、[0,+∞) |
| B、(-2,0] |
| C、(-2,+∞) |
| D、(-∞,-2)∪[0,+∞) |