题目内容
设口袋中有黑球、白球共7 个,从中任取两个球,令取到白球的个数为ξ,且ξ的数学期望Eξ=
,则口袋中白球的个数为 .
| 6 |
| 7 |
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:设口袋中有白球x个,由已知得ξ的可能取值为0,1,2,由Eξ=
,得
+
×2=
,由此能求出口袋中白球的个数.
| 6 |
| 7 |
| ||||
|
| ||
|
| 6 |
| 7 |
解答:
解:设口袋中有白球x个,
由已知得ξ的可能取值为0,1,2,
P(ξ=0)=
,
P(ξ=1)=
,
P(ξ=2)=
,
∵Eξ=
,∴
+
×2=
,
解得x=3.
∴口袋中白球的个数为3.
故答案为:3.
由已知得ξ的可能取值为0,1,2,
P(ξ=0)=
| ||
|
P(ξ=1)=
| ||||
|
P(ξ=2)=
| ||
|
∵Eξ=
| 6 |
| 7 |
| ||||
|
| ||
|
| 6 |
| 7 |
解得x=3.
∴口袋中白球的个数为3.
故答案为:3.
点评:本题考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要注意排列组合知识的合理运用.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
已知f(x)是定义在R上的奇函数,当x>0时,f(x)=log2x,则f(-8)值为( )
| A、3 | ||
B、
| ||
C、-
| ||
| D、-3 |
若复数Z1=1+i,Z2=3-i,则
=( )
| Z2 |
| Z1 |
| A、1+i | B、1+2i |
| C、1-2i | D、2-2i |
设函数f(x)=x3-22-x的零点为x0,则x0所在的大致区间是( )
| A、(3,4) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
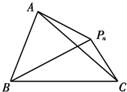 如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3;1,
如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3;1,| PnA |
| xn+1 |
| 3 |
| PnB |
| PnC |
( )
| A、65 | B、63 | C、33 | D、31 |
集合M={x|(
)x≥1},N={x|y=lg(x+2)},则M∩N等于( )
| 1 |
| 2 |
| A、[0,+∞) |
| B、(-2,0] |
| C、(-2,+∞) |
| D、(-∞,-2)∪[0,+∞) |
 已知三棱柱ABC-A1B1C1.
已知三棱柱ABC-A1B1C1.