题目内容
由y=x2，y=
x2及x=1围成的图形的面积S= ．
| 1 |
| 4 |
考点：定积分在求面积中的应用
专题：计算题,导数的概念及应用
分析：利用定积分表示面积，再求出原函数，即可得出结论．
解答：
解：由题意，S=
(x2-
x2)dx=
x3
=
．
故答案为：
．
| ∫ | 1 0 |
| 1 |
| 4 |
| 1 |
| 4 |
| | | 1 0 |
| 1 |
| 4 |
故答案为：
| 1 |
| 4 |
点评：本题主要考查积分的几何意义，确定原函数是关键．
练习册系列答案
期末集结号系列答案
相关题目
直线x+y=0被圆（x-2）2+y2=4截得的弦长为（ ）
A、
| ||||
B、
| ||||
C、2
| ||||
| D、2 |
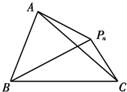如图，△ABC所在平面上的点Pn（n∈N*）均满足△PnAB与△PnAC的面积比为3；1，| PnA |
| xn+1 |
| 3 |
| PnB |
| PnC |
（ ）
| A、65 | B、63 | C、33 | D、31 |
若函数f（x）唯一的一个零点同时在（0，8），（4，8），（6，8）内，则下列结论正确的是（ ）
| A、函数f（x）在区间（7，8）内有零点 |
| B、函数f（x）在区间（6，7）或（7，8）内有零点 |
| C、函数f（x）在区间（0，7）内无零点 |
| D、函数f（x）在区间（0，6]上无零点 |
某中学从高三甲、乙两个班中各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生成绩的众数是83，乙班学生成绩的中位数是86，则x+y的值为（ ）