题目内容
设数列{3n-1an}的前n项和为Sn,且Sn=
,a∈N*.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=
,求数列{bn}的前n项和Tn.
| n |
| 3 |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=
| n |
| an |
考点:数列的求和
专题:等差数列与等比数列
分析:(I)由已知条件得到Sn=a1+3a2+32a3+…+3n-1an=
,求出Sn-1的表达式,两式相减能求出数列{an}的通项公式.
(II) 由(Ⅰ)得 bn=n•3n,由此利用错位相减法能求出数列{bn}的前n项和Tn.
| n |
| 3 |
(II) 由(Ⅰ)得 bn=n•3n,由此利用错位相减法能求出数列{bn}的前n项和Tn.
解答:
解:(I)∵数列{3n-1an}的前n项和为Sn,且Sn=
,a∈N*,
∴Sn=a1+3a2+32a3+…+3n-1an=
,①
Sn-1=a1+3a2+32a3+…+3n-2an-1=
(n≥2),②
①-②得3n-1an=
-
=
(n≥2).
∴an=
(n≥2).…(4分)
经验证n=1时也满足上式,
∴an=
(n∈N*).…(6分)
(II) 由(1)得 bn=n•3n,
Tn=1•3+2•32+3•33+…+n•3n,
3Tn=1•32+2•33+…+(n-1)•3n+n•3n+1,
两式相减得-2Tn=3+32+33+3n-n•3n+1,…(8分)
∴-2Tn=
-n•3n+1
=
-n•3n+1,
∴Tn=
•3n+1-
•3n+1+
•…(12分)
| n |
| 3 |
∴Sn=a1+3a2+32a3+…+3n-1an=
| n |
| 3 |
Sn-1=a1+3a2+32a3+…+3n-2an-1=
| n-1 |
| 3 |
①-②得3n-1an=
| n |
| 3 |
| n-1 |
| 3 |
| 1 |
| 3 |
∴an=
| 1 |
| 3n |
经验证n=1时也满足上式,
∴an=
| 1 |
| 3n |
(II) 由(1)得 bn=n•3n,
Tn=1•3+2•32+3•33+…+n•3n,
3Tn=1•32+2•33+…+(n-1)•3n+n•3n+1,
两式相减得-2Tn=3+32+33+3n-n•3n+1,…(8分)
∴-2Tn=
| 3-3n+1 |
| 1-3 |
=
| 3n+1-3 |
| 2 |
∴Tn=
| n |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,是中档题,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
相关题目
在△ABC中,角A、B、C的对边分别是a、b、c.若asinA+csinC-
asinC=bsinB.则角B等于( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
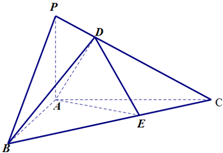 如图,在△ABC中,∠BAC=90°,AC=2AB,PA垂直△ABC所在的平面,PC与△ABC所在的平面成30°角,点D在线段PC上,点E在线段BC上.
如图,在△ABC中,∠BAC=90°,AC=2AB,PA垂直△ABC所在的平面,PC与△ABC所在的平面成30°角,点D在线段PC上,点E在线段BC上. 如图所示,ABCDEF是边长为1的正六边形,现从六个顶点任取三个顶点构成三角形,该三角形的面积S是一随机变量.
如图所示,ABCDEF是边长为1的正六边形,现从六个顶点任取三个顶点构成三角形,该三角形的面积S是一随机变量.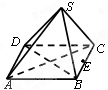 如图,正四棱锥S-ABCD中,AB=2,E是边BC的中点,动点P在四棱锥的表面上运动,且总保持
如图,正四棱锥S-ABCD中,AB=2,E是边BC的中点,动点P在四棱锥的表面上运动,且总保持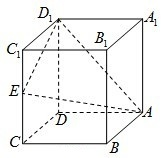 如图,在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面B1BCC1上的动点,并且A1F∥平面AED1,则动点F的轨迹是( )
如图,在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面B1BCC1上的动点,并且A1F∥平面AED1,则动点F的轨迹是( )