题目内容
函数f(x)=lnx+
x的零点所在的区间是( )
| 1 |
| 3 |
| A、(1,+∞) | ||
B、(
| ||
C、(0,
| ||
| D、(-1,0) |
考点:函数零点的判定定理
专题:计算题,函数的性质及应用
分析:由题意知函数f(x)=lnx+
x是定义域上的增函数,且连续;从而由零点判定定理判断.
| 1 |
| 3 |
解答:
解:易知函数f(x)=lnx+
x是定义域上的增函数,且连续;
而f(
)=-1+
•
<0,
f(1)=
>0;
故函数f(x)=lnx+
x的零点所在的区间是(
,1);
故选:B.
| 1 |
| 3 |
而f(
| 1 |
| e |
| 1 |
| 3 |
| 1 |
| e |
f(1)=
| 1 |
| 3 |
故函数f(x)=lnx+
| 1 |
| 3 |
| 1 |
| e |
故选:B.
点评:本题考查了函数的零点的判定定理的应用,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=3-2|x|,g(x)=x2,构造函数F(x)=
,那么函数y=F(x)( )
|
| A、有最大值1,最小值-1 |
| B、有最小值-1,无最大值 |
| C、有最大值1,无最小值 |
| D、有最大值3,最小值1 |
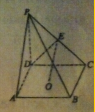
 如图,A、B两点都在河的对岸(不可到达),某人想测量A、B之间的距离,但只有卷尺和测角仪两种工具,若此人在地面上选一条基线EF,用卷尺测得EF的长度为a,且用测角仪测量了一些角度:∠AEB=α,∠AEF=β,∠BFE=γ,∠AFB=δ.请你用文字和公式写出计算A、B之间距离的步骤.
如图,A、B两点都在河的对岸(不可到达),某人想测量A、B之间的距离,但只有卷尺和测角仪两种工具,若此人在地面上选一条基线EF,用卷尺测得EF的长度为a,且用测角仪测量了一些角度:∠AEB=α,∠AEF=β,∠BFE=γ,∠AFB=δ.请你用文字和公式写出计算A、B之间距离的步骤.