题目内容
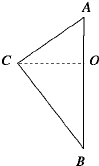 如图,在三角形ABC中,若AC=3,BC=4,AB=5,以AB所在直线为轴,将此三角形旋转一周,求所得旋转体的表面积和体积.
如图,在三角形ABC中,若AC=3,BC=4,AB=5,以AB所在直线为轴,将此三角形旋转一周,求所得旋转体的表面积和体积.考点:旋转体(圆柱、圆锥、圆台),棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:由已知中,AC=3,BC=4,AB=5,可得三角形ABC为直角三角形,我们可以判断出以斜边AB为轴旋转一周,所得旋转体的形状是AB边的高CO为底面半径的两个圆锥组成的组合体,计算出底面半径及两个圆锥高的和,代入圆锥体积公式,即可求出旋转体的体积;又由该几何体的表面积是两个圆锥的侧面积之和,分别计算出两个圆锥的母线长,代入圆锥侧面积公式,即可得到答案.
解答:
解:∵在三角形ABC中,若AC=3,BC=4,AB=5,
∴三角形ABC为直角三角形,
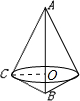
如图以斜边AB为轴旋转一周,得旋转体是以AB边的高CO为底面半径的两个圆锥组成的组合体
∵AC=3,BC=4,AB=5,
∴CO=
=
,
故此旋转体的体积V=
•πr2•h=
•π•CO2•AB=
π …6分
(2)又∵AC=3,BC=4,
故此旋转体的表面积
S=πr•(l+l′)=2πCO•(AC+BC)=
∴三角形ABC为直角三角形,
如图以斜边AB为轴旋转一周,得旋转体是以AB边的高CO为底面半径的两个圆锥组成的组合体

∵AC=3,BC=4,AB=5,
∴CO=
| AC•BC |
| AB |
| 12 |
| 5 |
故此旋转体的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 48 |
| 5 |
(2)又∵AC=3,BC=4,
故此旋转体的表面积
S=πr•(l+l′)=2πCO•(AC+BC)=
| 84π |
| 5 |
点评:本题考查的知识点是旋转体,圆锥的体积和表面积,其中根据已知判断出旋转所得旋转体的形状及底面半径,高,母线长等关键几何量,是解答本题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
已知f(x)=
,则下列结论成立的是( )
|
| A、f(x)在x=0处连续 | ||
B、
| ||
C、
| ||
D、
|
若<
,
>=60°,|
|=4,(
+2
)•(
-3
)=-72,则|
|=( )
| a |
| b |
| b |
| a |
| b |
| a |
| b |
| a |
| A、2 | B、4 | C、6 | D、12 |
一个几何体的三视图如图所示,则这个几何体的表面积为( )
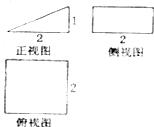

A、6+
| ||
B、6+2
| ||
C、8+
| ||
D、8+2
|
 锐角△ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为内切圆I与边CA的切点.若∠C=50°,则∠IEH的度数=
锐角△ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为内切圆I与边CA的切点.若∠C=50°,则∠IEH的度数=