题目内容
设函数f(x)=
在x=-1处取得极值-2.
(1)求f(x)的解析式;
(2)m为何值时,函数f(x)在区间(m,2m+1)上单调递增?
(3)若直线l与f(x)的图象相切于P(x0,y0),求l的斜率k的取值范围.
| ax |
| x2+b |
(1)求f(x)的解析式;
(2)m为何值时,函数f(x)在区间(m,2m+1)上单调递增?
(3)若直线l与f(x)的图象相切于P(x0,y0),求l的斜率k的取值范围.
考点:利用导数研究曲线上某点切线方程,函数解析式的求解及常用方法,函数单调性的判断与证明
专题:综合题,导数的综合应用
分析:(1)先对函数f(x)进行求导,根据函数f(x)在x=-1处取得极值-2,建立两个等式关系,求出两个变量a,b即可;
(2)求出导数,令导函数大于0,即可得到函数的递增区间,又由函数f(x)在(m,2m+1)上是增函数,则(m,2m+1)为递增区间的子集,建立关于参数m的不等式,解出即可求得结论;
(3)直线l的斜率为k=f′(x0)=4[
-
],换元,即可求l的斜率k的取值范围.
(2)求出导数,令导函数大于0,即可得到函数的递增区间,又由函数f(x)在(m,2m+1)上是增函数,则(m,2m+1)为递增区间的子集,建立关于参数m的不等式,解出即可求得结论;
(3)直线l的斜率为k=f′(x0)=4[
| 2 |
| (x02+1)2 |
| 1 |
| x02+1 |
解答:
解:(1)∵函数f(x)=
,∴f′(x)=
又函数f(x)=
在x=-1处取得极值-2,∴
,
解得:a=4,b=1,
∴f(x)=
…2分
(2)∵f′(x)=
,
令f′(x)>0,解得-1<x<1
∴函数f(x)的递增区间为(-1,1).
又∵f(x)在(m,2m+1)上单调递增,
∴
,解得-1≤m≤0.
∵在区间(m,2m+1)中2m+1>m,∴m>-1.
综上,-1<m≤0.…5分
(3)∵f′(x)=
,
∴直线l的斜率为k=f′(x0)=4[
-
]…10分
令
=t,t∈(0,1],∴k=4(2t2-t)∈[-
,4]…12分
| ax |
| x2+b |
| a(b-x2) |
| (x2+b)2 |
又函数f(x)=
| ax |
| x2+b |
|
解得:a=4,b=1,
∴f(x)=
| 4x |
| x2+1 |
(2)∵f′(x)=
| 4(1-x2) |
| (x2+1)2 |
令f′(x)>0,解得-1<x<1
∴函数f(x)的递增区间为(-1,1).
又∵f(x)在(m,2m+1)上单调递增,
∴
|
∵在区间(m,2m+1)中2m+1>m,∴m>-1.
综上,-1<m≤0.…5分
(3)∵f′(x)=
| 4(1-x2) |
| (x2+1)2 |
∴直线l的斜率为k=f′(x0)=4[
| 2 |
| (x02+1)2 |
| 1 |
| x02+1 |
令
| 1 |
| x02+1 |
| 1 |
| 2 |
点评:本题主要考查了利用导数研究函数的极值,考查利用导数研究函数的单调性,属于中档题.

练习册系列答案
相关题目
已知简谐振动f(x)=Asin(ωx+φ)(|φ|<
)的振幅为
,图象上相邻最高点与最低点之间的距离为5,且过点(0,
),则该简谐振动的频率与初相分别为( )
| π |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
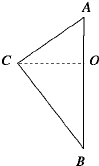 如图,在三角形ABC中,若AC=3,BC=4,AB=5,以AB所在直线为轴,将此三角形旋转一周,求所得旋转体的表面积和体积.
如图,在三角形ABC中,若AC=3,BC=4,AB=5,以AB所在直线为轴,将此三角形旋转一周,求所得旋转体的表面积和体积.