题目内容
椭圆的焦点为F1、F2,过点F1作直线与椭圆相交,被椭圆截得的最短的线段MN长为
,△MF2N的周长为20,则椭圆的离心率为 .
| 32 |
| 5 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:运用椭圆的定义,可得4a=20,解得a,再由直线垂直于x轴时,弦长最短,求出弦长,解得b,进而得到c,再由离心率公式,即可得到.
解答:
解:设椭圆方程为
+
=1(a>b>0),
则由椭圆的定义,可得,MF1+MF2=NF1+NF2=2a,
由于△MF2N的周长为20,则4a=20,即a=5,
过点F1作直线与椭圆相交,当直线垂直于x轴时,弦长最短,
令x=-c,代入椭圆方程,解得,y=±
,
即有
=
,解得,b2=16,c2=9,
则离心率e=
=
.
故答案为:
.
| x2 |
| a2 |
| y2 |
| b2 |
则由椭圆的定义,可得,MF1+MF2=NF1+NF2=2a,
由于△MF2N的周长为20,则4a=20,即a=5,
过点F1作直线与椭圆相交,当直线垂直于x轴时,弦长最短,
令x=-c,代入椭圆方程,解得,y=±
| b2 |
| a |
即有
| 2b2 |
| a |
| 32 |
| 5 |
则离心率e=
| c |
| a |
| 3 |
| 5 |
故答案为:
| 3 |
| 5 |
点评:本题考查椭圆的方程和性质及定义,考查离心率的求法,考查运算能力,属于中档题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
若有一组数据的总偏差平方和为120,相关指数为0.6,则回归平方和为( )
| A、60 | B、72 | C、48 | D、120 |
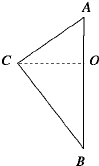 如图,在三角形ABC中,若AC=3,BC=4,AB=5,以AB所在直线为轴,将此三角形旋转一周,求所得旋转体的表面积和体积.
如图,在三角形ABC中,若AC=3,BC=4,AB=5,以AB所在直线为轴,将此三角形旋转一周,求所得旋转体的表面积和体积.