题目内容
设函数f(x)=|2x+1|-|x-4|.
(1)将函数f(x)写成分段函数的形式;
(2)画出函数f(x)的图象;
(3)写出函数f(x)的单调区间及值域.
(1)将函数f(x)写成分段函数的形式;
(2)画出函数f(x)的图象;
(3)写出函数f(x)的单调区间及值域.
考点:分段函数的应用
专题:数形结合,函数的性质及应用
分析:(1)去掉绝对值,化函数f(x)为分段函数;
(2)根据解析式,画出函数f(x)的图象即可;
(3)根据函数f(x)的图象,写出单调区间和值域.
(2)根据解析式,画出函数f(x)的图象即可;
(3)根据函数f(x)的图象,写出单调区间和值域.
解答:
 解:(1)∵函数f(x)=|2x+1|-|x-4|,
解:(1)∵函数f(x)=|2x+1|-|x-4|,
∴去掉绝对值,化为分段函数f(x)=
;
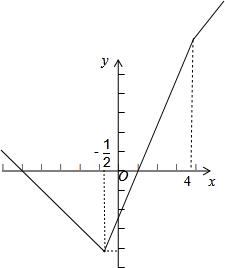
(2)根据解析式,画出函数f(x)的图象,如图所示;
(3)根据函数f(x)的图象,得出单调减区间是(-∞,-
],增区间是[-
,+∞);
值域是[-
,+∞).
 解:(1)∵函数f(x)=|2x+1|-|x-4|,
解:(1)∵函数f(x)=|2x+1|-|x-4|,∴去掉绝对值,化为分段函数f(x)=
|
(2)根据解析式,画出函数f(x)的图象,如图所示;
(3)根据函数f(x)的图象,得出单调减区间是(-∞,-
| 1 |
| 2 |
| 1 |
| 2 |
值域是[-
| 9 |
| 2 |
点评:本题考查了函数的图象与性质的应用问题,解题时先去掉绝对值,化函数为分段函数,画出函数的图象,结合函数的图象,解答问题,是基础题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目