题目内容
椭圆的两个焦点坐标分别为F1(-
,0)和F2(
,0),且椭圆过点(1,-
).
(1)求椭圆方程;
(2)过点(-
,0)作不与y轴垂直的直线l交该椭圆于M,N两点,A为椭圆的左顶点,求证:∠MAN=
.
| 3 |
| 3 |
| ||
| 2 |
(1)求椭圆方程;
(2)过点(-
| 6 |
| 5 |
| π |
| 2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意可设椭圆的方程为
+
=1(a>b>0).根据椭圆的两个焦点坐标分别为F1(-
,0)和F2(
,0),且椭圆过点(1,-
).可得
,解出即可.
(2)设直线MN的方程为x=ky-
,与椭圆的方程联立可得根与系数的关系,只要证明
•
=0即可.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 3 |
| ||
| 2 |
|
(2)设直线MN的方程为x=ky-
| 6 |
| 5 |
| AM |
| AN |
解答:
解:(1)由题意可设椭圆的方程为
+
=1(a>b>0).
∵椭圆的两个焦点坐标分别为F1(-
,0)和F2(
,0),且椭圆过点(1,-
).
∴
,解得c=
,b2=1,a2=4.
∴椭圆的方程为
+y2=1.
(2)证明:设直线MN的方程为x=ky-
,
联立
,
得(k2+4)y2-
ky-
=0,
设M(x1,y1),N(x2,y2),A(-2,0),
y1y2=-
,y1+y2=
,
则
•
=(x1+2,y1)•(x2+2,y2)
=(k2+1)y1y2+
k(y1+y2)+
=0,
即可得∠MAN=
.
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆的两个焦点坐标分别为F1(-
| 3 |
| 3 |
| ||
| 2 |
∴
|
| 3 |
∴椭圆的方程为
| x2 |
| 4 |
(2)证明:设直线MN的方程为x=ky-
| 6 |
| 5 |
联立
|
得(k2+4)y2-
| 12 |
| 5 |
| 64 |
| 25 |
设M(x1,y1),N(x2,y2),A(-2,0),
y1y2=-
| 64 |
| 25(k2+4) |
| 12k |
| 5(k2+4) |
则
| AM |
| AN |
=(k2+1)y1y2+
| 4 |
| 5 |
| 16 |
| 25 |
即可得∠MAN=
| π |
| 2 |
点评:本题考查了椭圆的标准方程与性质、直线与椭圆相交问题转化方程联立可得根与系数的关系、向量垂直与数量积的关系等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
在(x2-
)9的二项式展开式中,常数项是( )
| 1 |
| x |
| A、504 | B、84 |
| C、-84 | D、-504 |
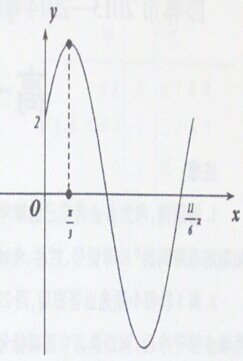 已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ< 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2.