题目内容
已知数列{an}的通项公式为an=n+2,若将数列{an}的项重新组合,得到新数列{bn},具体方法如下:b1=a1,b2=a2+a3,b3=a4+a5+a6+a7,b4=a8+a9+a10+…a15,…,依此类推,第n项bn由相应的{an}中2n-1项的和组成.
(1)求数列{bn-
•2n}的前n项和Tn;
(2)设数列{cn}的通项公式cn=
,求数列{cn}的最小项.
(1)求数列{bn-
| 1 |
| 4 |
(2)设数列{cn}的通项公式cn=
| bn-3×2n-2 +24 |
| 2n-3 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由题意得bn=a2n-1+aan-1+1+…+a2n-1+2n-1-1,由此求出bn-
•2n=22n-2+22n-3+2n-1=
•4n+
•2n,从而能求出数列{bn-
•2n}的前n项和Tn.
(2)cn=
=
=3•2n+
-2,利用均值定理能求出数列{cn}的最小项是第3项.
| 1 |
| 4 |
| 3 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
(2)cn=
| bn-3×2n-2 +24 |
| 2n-3 |
| ||||
|
| 192 |
| 2n |
解答:
解:(1)由题意得bn=a2n-1+aan-1+1+…+a2n-1+2n-1-1
=(2n-1+2)+(2n-1+3)+…+(2n-1+2n-1+1)
=2n-1•2n-1+(2+3+…+2n-1+1)
=22n-2+
(2n-1+3)
=22n-2+2n-2(2n-1+3).
∴bn-
•2n=22n-2+22n-3+2n-1=
•4n+
•2n.
∴Tn=
•
+
•
=
(4n-1)+2n-1
=22n-1+2n-
.
(2)cn=
=
=
=3•2n+
-2
≥2
-2
=50.
当且仅当2n=8即n=3时,取等号.
∴数列{cn}的最小项是第3项.
=(2n-1+2)+(2n-1+3)+…+(2n-1+2n-1+1)
=2n-1•2n-1+(2+3+…+2n-1+1)
=22n-2+
| 2n-1 |
| 2 |
=22n-2+2n-2(2n-1+3).
∴bn-
| 1 |
| 4 |
| 3 |
| 8 |
| 1 |
| 2 |
∴Tn=
| 3 |
| 8 |
| 4(1-4n) |
| 1-4 |
| 1 |
| 2 |
| 2(1-2n) |
| 1-2 |
=
| 1 |
| 2 |
=22n-1+2n-
| 3 |
| 2 |
(2)cn=
| bn-3×2n-2 +24 |
| 2n-3 |
| ||||
|
=
| 3•4n-2•2n+192 |
| 2n |
| 192 |
| 2n |
≥2
3•2n×
|
=50.
当且仅当2n=8即n=3时,取等号.
∴数列{cn}的最小项是第3项.
点评:本题考查数列的数列的前n项和的求法,考查数一铁最小项的求法,是中档题,解题时要认真审题,注意均值定理的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
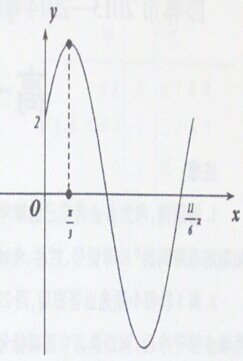 已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ< 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2.