题目内容
 如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE
如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE(1)设M为线段A1C的中点,求证:BM∥平面A1DE;
(2)当平面A1DE⊥平面BCD时,求直线CD与平面A1CE所成角的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)取CD中点N,并连接MN,BN,容易证明平面BMN∥平面A1DE,所以便得到BM∥平面A1DE;
(2)容易说明CE⊥平面A1DE,所以DA1⊥CE,又DA1⊥A1E,所以DA1⊥平面A1CE,所以∠A1CD便是直线CD与平面A1CE所成角,所以该角的正弦值为
=
=
.
(2)容易说明CE⊥平面A1DE,所以DA1⊥CE,又DA1⊥A1E,所以DA1⊥平面A1CE,所以∠A1CD便是直线CD与平面A1CE所成角,所以该角的正弦值为
| A1D |
| CD |
| 2 |
| 4 |
| 1 |
| 2 |
解答:
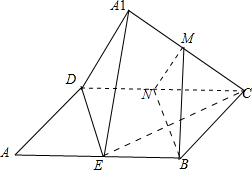 解:(1)证明:如图,取CD中点N,连接MN,BN,∵M为A1C的中点,∴MN∥A1D,A1D?平面A1DE,∴MN∥平面A1DE;
解:(1)证明:如图,取CD中点N,连接MN,BN,∵M为A1C的中点,∴MN∥A1D,A1D?平面A1DE,∴MN∥平面A1DE;
∵E为AB的中点,四边形ABCD为矩形,∴DN∥BE,且DN=BE,∴四边形BEDN为平行四边形;
∴BN∥ED,ED?平面A1DE,∴BN∥平面A1DE,MN∩BN=N;
∴平面BMN∥平面A1DE,BM?平面BMN,∴BM∥平面A1DE;
(2)根据已知条件知:△ADE,和△BCN都是等腰直角三角形,∠AED=∠BEC=45°,∴∠CED=90°即CE⊥DE;
∵平面A1DE⊥平面BCD,且平面A1DE∩平面BCD=DE,CE?平面BCD;
∴CE⊥平面A1DE,DA1?平面A1DE,∴CE⊥DA1,即DA1⊥CE,又∠EAD=∠DA1E=90°,即DA1⊥A1E,A1E∩CE=E;
∴DA1⊥平面A1CE;
∴∠DCA1即是直线CD与平面A1CE所成的角,∴sin∠DCA1=
=
=
;
即直线CD与平面A1CE所成角的正弦值为
.
 解:(1)证明:如图,取CD中点N,连接MN,BN,∵M为A1C的中点,∴MN∥A1D,A1D?平面A1DE,∴MN∥平面A1DE;
解:(1)证明:如图,取CD中点N,连接MN,BN,∵M为A1C的中点,∴MN∥A1D,A1D?平面A1DE,∴MN∥平面A1DE;∵E为AB的中点,四边形ABCD为矩形,∴DN∥BE,且DN=BE,∴四边形BEDN为平行四边形;
∴BN∥ED,ED?平面A1DE,∴BN∥平面A1DE,MN∩BN=N;
∴平面BMN∥平面A1DE,BM?平面BMN,∴BM∥平面A1DE;
(2)根据已知条件知:△ADE,和△BCN都是等腰直角三角形,∠AED=∠BEC=45°,∴∠CED=90°即CE⊥DE;
∵平面A1DE⊥平面BCD,且平面A1DE∩平面BCD=DE,CE?平面BCD;
∴CE⊥平面A1DE,DA1?平面A1DE,∴CE⊥DA1,即DA1⊥CE,又∠EAD=∠DA1E=90°,即DA1⊥A1E,A1E∩CE=E;
∴DA1⊥平面A1CE;
∴∠DCA1即是直线CD与平面A1CE所成的角,∴sin∠DCA1=
| DA1 |
| CD |
| 2 |
| 4 |
| 1 |
| 2 |
即直线CD与平面A1CE所成角的正弦值为
| 1 |
| 2 |
点评:考查线面平行的判定定理,面面平行的判定定理,及面面平行的性质,面面垂直的性质定理,线面垂直的判定定理,线面角的定义及求法.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
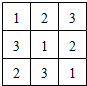 (1)如图,将1,2,3填入3×3的方格中,要求每行、每列都没有重复数字,右面是一种填法,则不同的填写方法共有几种?(用数字作答).
(1)如图,将1,2,3填入3×3的方格中,要求每行、每列都没有重复数字,右面是一种填法,则不同的填写方法共有几种?(用数字作答).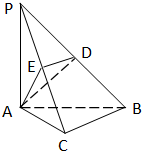 如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别是棱PB、PC的中点.
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别是棱PB、PC的中点.