题目内容
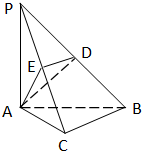 如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别是棱PB、PC的中点.
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别是棱PB、PC的中点.(Ⅰ)求证:DE∥平面ABC;
(Ⅱ)求证:平面PBC⊥平面PAC.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(Ⅰ)借助三角形内的中位线证明线线平行,进而证明线面平行;
(Ⅱ)由线面垂直证明线线垂直,再由线线垂直证明线面垂直,进而证明面面垂直.
(Ⅱ)由线面垂直证明线线垂直,再由线线垂直证明线面垂直,进而证明面面垂直.
解答:
证明:(Ⅰ)在△PBC中,
∵点D、E分别是棱PB、PC的中点,
∴DE∥BC,
又∵DE?平面ABC,BC?平面ABC;
∴DE∥平面ABC.
(Ⅱ)∵PA⊥底面ABC,
∴PA⊥BC,
又∵∠BCA=90°,
∴BC⊥AC,
∴BC⊥平面PAC,
∴平面PBC⊥平面PAC.
∵点D、E分别是棱PB、PC的中点,
∴DE∥BC,
又∵DE?平面ABC,BC?平面ABC;
∴DE∥平面ABC.
(Ⅱ)∵PA⊥底面ABC,
∴PA⊥BC,
又∵∠BCA=90°,
∴BC⊥AC,
∴BC⊥平面PAC,
∴平面PBC⊥平面PAC.
点评:本题考查了线面平行,面面垂直的证明,属于基础题.

练习册系列答案
相关题目
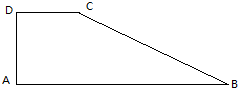 如图,一直角梯形ABCD的上,上下底分别为CD=
如图,一直角梯形ABCD的上,上下底分别为CD= 如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE
如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE