题目内容
下列说法:
①已知
是单位向量|
+
|=|
-2
|,则
在
方向上的投影为
;
②函数f(x)=
的对称中心是(-
,-
);
③将函数y=sin(2x+
)图象向右平移
个单位,得到函数y=2sin2x的图象;
④在△ABC中,若A<B,则sinA<sinB;
其中正确的命题序号是 (填出所有正确命题的序号).
①已知
. |
| e |
. |
| a |
. |
| e |
. |
| a |
. |
| e |
| a |
| e |
| 1 |
| 2 |
②函数f(x)=
| x-1 |
| 2x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
③将函数y=sin(2x+
| π |
| 3 |
| π |
| 3 |
④在△ABC中,若A<B,则sinA<sinB;
其中正确的命题序号是
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:化简①由已知化简可得
•
=
2,而要求的等于|
|cos<
,
>,代入化简,即可判断正误;利用分离常数法,对函数的解析式进行变形,进而求出对称中心,可判断②;根据函数图象的平移变换法则,求出平移后函数的解析式,可判断③;根据正弦定理,及三角形大角对大边的性质,可判断④.
| a |
| e |
| 1 |
| 2 |
| e |
| a |
| a |
| e |
解答:
解:对于①,∵|
+
|=|
-2
|,
∴(|
+
|)2=(|
-2
|)2,
展开化简可得:
•
=
2,
故
在
方向上的投影等于|
|cos<
,
>=
=
,所以①正确.
对于②,函数f(x)=
=
+
,其中x≠-
,y≠
,故函数f(x)=
的对称中心是(-
,
),故②错误;
对于③,将函数y=sin(2x+
)图象向右平移
个单位,得到函数y=2sin[2(x-
)+
]=sin(2x-
)的图象,故③错误;
对于④在△ABC中,若A<B,则a<b,即2RsinA<2RsinB,即sinA<sinB,故④正确.
故正确的命题序号是:①④,
故答案为:①④
| a |
| e |
| a |
| e |
∴(|
| a |
| e |
| a |
| e |
展开化简可得:
| a |
| e |
| 1 |
| 2 |
| e |
故
| a |
| e |
| a |
| a |
| e |
| ||||
|
|
| 1 |
| 2 |
对于②,函数f(x)=
| x-1 |
| 2x+1 |
| 1 |
| 2 |
-
| ||
| 2x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| x-1 |
| 2x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
对于③,将函数y=sin(2x+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
对于④在△ABC中,若A<B,则a<b,即2RsinA<2RsinB,即sinA<sinB,故④正确.
故正确的命题序号是:①④,
故答案为:①④
点评:本题以命题的真假判断为载体,考查了向量的投影与数量积运算,函数的对称性,函数图象的平移变换,正弦定理,难度中档.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
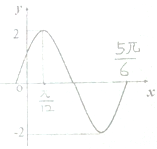 函数f(x)=Asin(ωx+φ)(ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(ω>0,|φ|<