题目内容
7.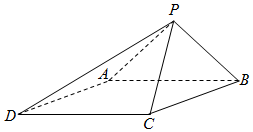 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.(Ⅰ)线段AB上是否存在点M,使AB⊥平面PCM?并给出证明.
(Ⅱ)求直线PB与平面PCD的正弦值.
分析 (Ⅰ)利用当M是AB的中点时,AB⊥平面PCM,证明AB⊥PM,AB⊥CM,即可证明.
(Ⅱ)过点M作MN⊥PC交PC于点N,点M与B到平面PMC的距离相等,即可求直线PB与平面PCD的正弦值.
解答 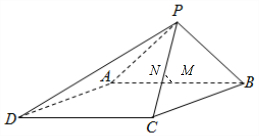 解:(Ⅰ)当M是AB的中点时,AB⊥平面PCM…(1分)
解:(Ⅰ)当M是AB的中点时,AB⊥平面PCM…(1分)
∵AP=PB,∴AB⊥PM
又△ACB中,AB=BC,∠ABC=60°,∴△ABC是正三角形,∴AB⊥CM
又 PM∩CM=M,∴AB⊥平面PCM…(4分)
(Ⅱ) 过点M作MN⊥PC交PC于点N,
由AB⊥平面PCM,AB∥CD得,CD⊥平面PCM
又CD?平面PCD,∴平面PCD⊥平面PCM
又MN?平面PCD,∴MN⊥平面PCD…(6分)
由已知可得$MP=1,MC=\sqrt{3}$,在Rt△PCM中,由面积公式得PM=$\frac{\sqrt{3}}{2}$,…(8分)
又AB∥CD,AB?平面PCM,∴AB∥平面PCM
即点M与B到平面PMC的距离相等,即为$\frac{{\sqrt{3}}}{2}$,…(10分)
又PB=3,∴PB与平面PCD所成角的正弦值为$\frac{{\sqrt{6}}}{4}$,…(12分)
点评 本题考查线面垂直,考查线面角,考查学生分析解决问题的能力,正确运用线面垂直的判定定理是关键.

练习册系列答案
相关题目
3.已知抛物线y2=20x的焦点F恰好为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点,且点F到双曲线的渐近线的距离是4,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{41}$$-\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{21}$$-\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{3}$$-\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{9}$$-\frac{{y}^{2}}{16}$=1 |
15.f(x)是定义在(0,+∞)上的单调函数,且对?x∈(0,+∞)都有f(f(x)-lnx)=e+1,则方程f(x)-f′(x)=e的实数解所在的区间是( )
| A. | (0,$\frac{1}{e}$) | B. | ($\frac{1}{e}$,1) | C. | (1,e) | D. | (e,4) |
2.已知命题p:“?x∈R,使”4x+2x+1-m=0”,若“¬p”为假命题,则实数m的取值范围是( )
| A. | (-1,+∞) | B. | (0,+∞) | C. | [0,+∞) | D. | [1,+∞) |
12.设集合A={x|(x+1)(4-x)>0},B={x|0<x<9},则A∩B等于( )
| A. | (0,4) | B. | (4,9) | C. | (-1,4) | D. | (-1,9) |
17.已知集合M={x|(x-1)=0},那么( )
| A. | 0∈M | B. | 1∉M | C. | -1∈M | D. | 0∉M |