题目内容
12.设集合A={x|(x+1)(4-x)>0},B={x|0<x<9},则A∩B等于( )| A. | (0,4) | B. | (4,9) | C. | (-1,4) | D. | (-1,9) |
分析 求出A中不等式的解集,找出A与B的交集即可.
解答 解:由A中不等式变形得:(x+1)(x-4)<0,
解得:-1<x<4,即A=(-1,4),
∵B=(0,9),
∴A∩B=(0,4),
故选:A.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
3.已知圆C:x2+y2-4x+m=0与圆${({x-3})^2}+{({y+2\sqrt{2}})^2}=4$外切,点P是圆C一动点,则点P到直线3x-4y+4=0的距离的最大值为( )
| A. | $2\sqrt{2}$ | B. | 3 | C. | 4 | D. | $3\sqrt{2}$ |
20.若存在正实数m,使得关于x的方程x+a(2x+2m-4ex)[1n(x+m)-lnx]=0有两个不同的根,其中e为自然对数的底数,则实数a的取值范围是( )
| A. | (-∞,0) | B. | (0,$\frac{1}{2e}$) | C. | (-∞,0)∪($\frac{1}{2e}$,+∞) | D. | ($\frac{1}{2e}$,+∞) |
4.已知抛物线C:y2=2px(0<p<4)的焦点为F,点P为C上一动点,A(4,0),B(p,$\sqrt{2}$p),且|PA|的最小值为$\sqrt{15}$,则|BF|等于( )
| A. | 4 | B. | $\frac{7}{2}$ | C. | 5 | D. | $\frac{9}{2}$ |
1.已知集合A={x|y=lg(x+1)},B={x||x|<2},则A∩B=( )
| A. | (-2,0) | B. | (0,2) | C. | (-1,2) | D. | (-2,-1) |
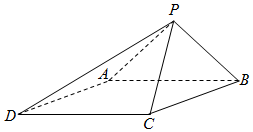 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.