题目内容
19.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>1)的焦距为2,过短轴的一个端点与两个焦点的圆的面积为$\frac{4}{3}$π,过椭圆C的右焦点作斜率为k(k≠0)的直线l与椭圆C相交于A、B两点,线段AB的中点为P.(1)求椭圆C的标准方程;
(2)过点P垂直于AB的直线与x轴交于点D($\frac{1}{7}$,0),求k的值.
分析 (1)根据题意,在三角形中由勾股定理列出等式,根据已知的焦距大小,即可求得椭圆方程;
(2)设过椭圆C的右焦点的直线l的方程为y=k(x-1),(k≠0),设A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{y=k(x-1)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$整理得:(4k2+3)x2-8k2x+4k2-12=0,由韦达定理得D坐标即可求k
解答 解:(1)过短轴的一个端点与两个焦点的圆的半径为$\frac{2}{\sqrt{3}}$,设右焦点的坐标为(c,0),
$\left\{\begin{array}{l}{2c=2}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{(b-\frac{2}{\sqrt{3}})^{2}+1=\frac{4}{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\{b=\sqrt{3}}\\{c=1}\end{array}\right.$.
椭圆C的标准方程:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)设过椭圆C的右焦点的直线l的方程为y=k(x-1),(k≠0),
设A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{y=k(x-1)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$整理得:(4k2+3)x2-8k2x+4k2-12=0,
由韦达定理得x1+x2=$\frac{8{k}^{2}}{3+4{k}^{2}}$,x1•x2=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$.
y1+y2=k(x1+x2)-2k=-$\frac{6k}{3+4{k}^{2}}$.
∵P为线段AB的中点,则可得点P($\frac{4{k}^{2}}{3+4{k}^{2}},\frac{-3k}{3+4{k}^{2}}$).
又直线PD的斜率为-$\frac{1}{k}$,直线PD的方程为:y-$\frac{-3k}{3+4{k}^{2}}$=-$\frac{1}{k}(x-\frac{4{k}^{2}}{3+4{k}^{2}})$.
令y=0得,x=$\frac{{k}^{2}}{3+4{k}^{2}}$,
∵AB的直线与x轴交于点D($\frac{1}{7}$,0),∴$\frac{{k}^{2}}{3+4{k}^{2}}=\frac{1}{7}$,解得k=±1.
点评 本题考查椭圆的标准方程及简单几何性质,考查直线与椭圆的位置关系,韦达定理,中点坐标公式,考查计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | {x|x>1} | B. | {x|x>0} | C. | {x|0<x<2} | D. | {x|1<x<2} |
| A. | A∩B=(0,1) | B. | A∪B=R | C. | B?A | D. | A=B |
| A. | c<b<a | B. | b<a<c | C. | a<b<c | D. | b<c<a |
| A. | 4 | B. | $\frac{7}{2}$ | C. | 5 | D. | $\frac{9}{2}$ |
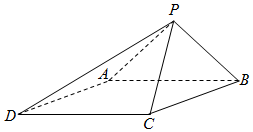 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.