题目内容
在△ABC中，AB=2，B=2C，则AC的取值范围是 ．
考点：正弦定理,三角函数中的恒等变换应用
专题：计算题,解三角形
分析：利用正弦定理，可得AC=4cosC，确定0°＜C＜60°，即可求出AC的取值范围．
解答：
解：∵在△ABC中，AB=2，B=2C，
∴
=
，
∴AC=4cosC，
∵0°＜C＜60°，
∴
＜cosC＜1，
∴2＜AC＜4，
故答案为：（2，4）
∴
| AB |
| sinC |
| AC |
| sin2C |
∴AC=4cosC，
∵0°＜C＜60°，
∴
| 1 |
| 2 |
∴2＜AC＜4，
故答案为：（2，4）
点评：本题考查AC的取值范围，考查正弦定理，考查学生的计算能力，比较基础．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目
已知集合A={x|x是菱形}，B={x|x是正方形}，C={心x|x是平行四边形}，那么A，B，C之间的关系是（ ）
| A、A⊆B⊆C |
| B、B⊆A⊆C |
| C、A?B⊆C |
| D、A=B⊆C |
若x1，x2是方程2x2-4x+1=0的两个根，则
+
的值为（ ）
| x1 |
| x2 |
| x2 |
| x1 |
| A、6 | ||
| B、4 | ||
| C、3 | ||
D、
|
已知△ABC中，a=
，b=1，B=30°，则△ABC的面积是（ ）
| 3 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
从装有2个白球和2个蓝球的口袋中任取2个球，那么对立的两个事件是（ ）
| A、“恰有一个白球”与“恰有两个白球” |
| B、“至少有一个白球”与“至少有-个蓝球” |
| C、“至少有-个白球”与“都是蓝球” |
| D、“至少有一个白球”与“都是白球” |
己知等差数列{an}的公差d=-1，若a2+a8=2，则该数列的前n项和Sn的最大值为（ ）
| A、5 | B、10 | C、15 | D、16 |
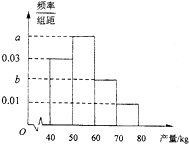果农随机选取某类果树50株作为样本测量它们每一株的果实产量（单位：kg），获得的所有数据按照区间（40，50]，（50，60]，（60，70]，（70，80]进行分组，得到频率分布直方图如图，已知样本中产量在区间（50，60]上的果树株数是产量在区间（60，80]上的果树株数的