题目内容
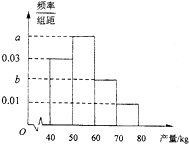 果农随机选取某类果树50株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,50],(50,60],(60,70],(70,80]进行分组,得到频率分布直方图如图,已知样本中产量在区间(50,60]上的果树株数是产量在区间(60,80]上的果树株数的
果农随机选取某类果树50株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,50],(50,60],(60,70],(70,80]进行分组,得到频率分布直方图如图,已知样本中产量在区间(50,60]上的果树株数是产量在区间(60,80]上的果树株数的| 4 |
| 3 |
(1)求a,b的值;
(2)估计该类果树的平均产量;
(3)为了进一步分析该类果树的情况,现要用分层抽样的方法,从中再抽取20株,那么在(60,70]区间内应抽取多少株?
考点:频率分布直方图,分层抽样方法
专题:概率与统计
分析:(1)根据频率分布直方图中各小长方形的面积和等于1,结合题意,求出a、b的值;
(2)根据频率分布直方图,估计该类果树的平均产量(平均值);
(3)根据分层抽样方法的特点,求出在(60,70]区间内应抽取的株数.
(2)根据频率分布直方图,估计该类果树的平均产量(平均值);
(3)根据分层抽样方法的特点,求出在(60,70]区间内应抽取的株数.
解答:
解:(1)根据题意,得;
(0.03+a+b+0.01)×10=1,
∴a+b=0.06,
又∵a=
(b+0.01),
∴a=0.04,b=0.02;
(2)根据频率分布直方图,估计该类果树的平均产量是
=45×0.03×10+55×0.04×10+65×0.02×10+75×0.01×10=56(kg);
(3)根据分层抽样方法的特点,从中抽取20株,
在(60,70]区间内应抽取20×0.02×10=4(株).
(0.03+a+b+0.01)×10=1,
∴a+b=0.06,
又∵a=
| 4 |
| 3 |
∴a=0.04,b=0.02;
(2)根据频率分布直方图,估计该类果树的平均产量是
. |
| x |
(3)根据分层抽样方法的特点,从中抽取20株,
在(60,70]区间内应抽取20×0.02×10=4(株).
点评:本题考查了频率分布直方图的应用问题,解题时应结合图形解答问题,是基础题.

练习册系列答案
相关题目
若正数a,b满足,直线ax+by=1与圆x2+y2=1相切,则a+b的最大值是( )
| A、4 | ||
B、2
| ||
| C、2 | ||
D、
|
已知函数f(x)=log2(2-ax)在(-∞,1]上单调递减,则a的取值范围是( )
| A、1<a<2 |
| B、0<a<1 |
| C、0<a<1或1<a<2 |
| D、0<a<1或a>2 |
 随机抽取某中学12位高三同学,调查他们春节期间购书费用(单位:元),获得数据的茎叶图如图,这12位同学购书费用的中位数是
随机抽取某中学12位高三同学,调查他们春节期间购书费用(单位:元),获得数据的茎叶图如图,这12位同学购书费用的中位数是