题目内容
5.定义在R上的奇函数f(x)满足x>0时,f(x)=x-$\sqrt{x}$+1.(1)求函数f(x)的解析式;
(2)求函数f(x)的值域.
分析 (1)根据题意,由奇函数的性质分析有f(0)=0;再令x<0,则有-x>0,分析可得f(x)=-f(-x)=-[(-x)-$\sqrt{-x}$+1]=x+$\sqrt{-x}$+1,综合可得函数的解析式;
(2)根据题意,由(1)的解析式分三种情况讨论:当x>0时,令t=$\sqrt{x}$>0,则有f(x)=x-$\sqrt{x}$+1=t2-t+1,由二次函数的性质分析可得此时值域,当x=0时,有f(0)=0,当x<0时,由奇函数的性质可得此时函数的值域,综合三种情况可得答案.
解答 解:(1)根据题意,f(x)为定义在R上的奇函数,则f(0)=0,
当x<0时,-x>0,
f(x)=-f(-x)=-[(-x)-$\sqrt{-x}$+1]=x+$\sqrt{-x}$-1,
故函数f(x)的解析式为f(x)=$\left\{\begin{array}{l}{x-\sqrt{x}+1,x>0}\\{0,x=0}\\{x+\sqrt{-x}-1,x<0}\end{array}\right.$,
(2)当x>0时,令t=$\sqrt{x}$>0,
则有f(x)=x-$\sqrt{x}$+1=t2-t+1=(t-$\frac{1}{2}$)2+$\frac{3}{4}$,
又由t>0,则有f(x)≥$\frac{3}{4}$,
当x=0时,有f(0)=0,
当x<0时,-x>0,f(x)=-f(-x),
而f(-x)≥$\frac{3}{4}$,则f(x)≤-$\frac{3}{4}$;
综合可得函数f(x)的值域为{y|y≥$\frac{3}{4}$或y≤-$\frac{3}{4}$或y=0}.
点评 本题考查函数奇偶性的应用,注意结合奇函数的性质求出解析式,不能忽略f(0)=0.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案| A. | 54 | B. | 108 | C. | 162 | D. | 324 |
| A. | {7,9} | B. | {1,3,7,9} | C. | {5} | D. | {1,3,5} |
| A. | 样本点都在回归直线上 | B. | 样本点都集中在回归直线附近 | ||
| C. | 样本点比较分散 | D. | 不存在规律 |

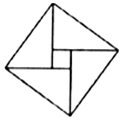 第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如下图会标是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较大的锐角为θ,那么$sin({θ+\frac{π}{3}})$=$\frac{{4+3\sqrt{3}}}{10}$.
第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如下图会标是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较大的锐角为θ,那么$sin({θ+\frac{π}{3}})$=$\frac{{4+3\sqrt{3}}}{10}$.