题目内容
求一次函数f（x），使f{f[f（x）]}=8x+7．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：设一次函数f（x）=ax+b，由题意可得a和b的方程组，解方程组可得．
解答：
解：设一次函数f（x）=ax+b，a≠0，
∵f{f[f（x）]}=8x+7，
∴a[a（ax+b）+b]+b=8x+7，
∴a3x+a2b+ab+b=8x+7，
∴
，解得
，
∴一次函数f（x）=2x+1
∵f{f[f（x）]}=8x+7，
∴a[a（ax+b）+b]+b=8x+7，
∴a3x+a2b+ab+b=8x+7，
∴
|
|
∴一次函数f（x）=2x+1
点评：本题考查函数解析式求解的待定系数法，涉及方程组的解法，属基础题．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
若集合A={x|
≤0}，B={x|x≥-2}且A⊆B．则实数a的取值范围是（ ）
| x-a |
| x-2 |
| A、（-∞，-2] |
| B、[-2，2] |
| C、[-2，+∞） |
| D、[2，+∞） |
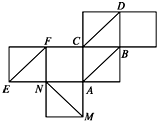如图为棱长是1的正方体的表面展开图，在原正方体中，给出下列三个命题：