题目内容
已知函数f(x)=
+
,g(n)=(
)n,(n∈N*),若f′(x)≥g(n)当x∈(-∞,λ]时恒成立.
(Ⅰ)当n=1时,求不等式f′(x)≥g(n)的解集;
(Ⅱ)求实常数λ的取值范围.
| x3 |
| 3 |
| x2 |
| 4 |
| 1 |
| 2 |
(Ⅰ)当n=1时,求不等式f′(x)≥g(n)的解集;
(Ⅱ)求实常数λ的取值范围.
考点:函数恒成立问题
专题:计算题,函数的性质及应用,导数的概念及应用,等差数列与等比数列
分析:(Ⅰ)求出导数,运用二次不等式的解法,即可得到解集;
(Ⅱ)若f′(x)≥g(n)当x∈(-∞,λ]时恒成立,则x2+
x≥g(n)max当x∈(-∞,λ]时恒成立.根据等比数列的单调性,即可得到最大值,再解不等式,由集合的包含关系,即可得到所求范围.
(Ⅱ)若f′(x)≥g(n)当x∈(-∞,λ]时恒成立,则x2+
| 1 |
| 2 |
解答:
解:(Ⅰ)n=1时,g(1)=
,
f′(x)=x2+
x,
不等式f′(x)≥g(n)即为x2+
x≥
,
解得,x≥
或x≤-1.
则解集为{x|x≥
或x≤-1};
(Ⅱ)若f′(x)≥g(n)当x∈(-∞,λ]时恒成立,
则x2+
x≥g(n)max当x∈(-∞,λ]时恒成立.
而g(n)=(
)n,(n∈N*)为递减数列,
则n=1时取得最大值
,
则x2+
x≥
当x∈(-∞,λ]时恒成立.
即有(-∞,λ]⊆(-∞,-1],
解得,λ≤-1.
则实常数λ的取值范围是(-∞,-1].
| 1 |
| 2 |
f′(x)=x2+
| 1 |
| 2 |
不等式f′(x)≥g(n)即为x2+
| 1 |
| 2 |
| 1 |
| 2 |
解得,x≥
| 1 |
| 2 |
则解集为{x|x≥
| 1 |
| 2 |
(Ⅱ)若f′(x)≥g(n)当x∈(-∞,λ]时恒成立,
则x2+
| 1 |
| 2 |
而g(n)=(
| 1 |
| 2 |
则n=1时取得最大值
| 1 |
| 2 |
则x2+
| 1 |
| 2 |
| 1 |
| 2 |
即有(-∞,λ]⊆(-∞,-1],
解得,λ≤-1.
则实常数λ的取值范围是(-∞,-1].
点评:本题考查导数的概念和运用,考查等比数列的单调性,考查二次不等式的解法,以及不等式恒成立思想转化为最值问题,考查运算能力,属于中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
“非p为假命”是“p且q是真命题”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也木必要条件 |
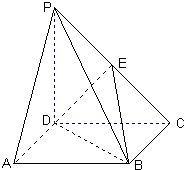 如图,四棱锥P-ABCD的底面ABCD是正方形,棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,棱PD⊥底面ABCD,PD=DC,E是PC的中点.