题目内容
已知函数f(x)=xex(e为自然对数的底数)
(1)求函数在x=1处的切线方程;
(2)若任意x∈R,f(x)>m恒成立,求实数m的取值范围.
(1)求函数在x=1处的切线方程;
(2)若任意x∈R,f(x)>m恒成立,求实数m的取值范围.
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)先求出切点的坐标,然后求出x=1处的导数,从而求出切线的斜率,利用点斜式方程即可求出切线方程.
(2)由题意可得,即求f(x)的最小值,利用导数先判断函数的单调性,求出最小值即得结论.
(2)由题意可得,即求f(x)的最小值,利用导数先判断函数的单调性,求出最小值即得结论.
解答:
解:(1)∵f(x)=xex
∴f′(x)=ex+xex,∴f′(1)=2e,又f(1)=e,
∴曲线y=f(x)在点(1,f(1))处的切线方程为y-e=2e(x-1),即2ex-y-e=0.
(2)∵任意x∈R,f(x)>m恒成立,
∴只要f(x)min>m即可,
令f′(x)>0⇒x>-1,即函数f(x)的单调递增区间是(-1,+∞);
由f′(x)<0⇒x<-1,即函数f(x)的单调递减区间是(-∞,-1);
∴当x=-1时,f(x)min=f(-1)=0,
∴实数m的取值范围(-∞,0).
∴f′(x)=ex+xex,∴f′(1)=2e,又f(1)=e,
∴曲线y=f(x)在点(1,f(1))处的切线方程为y-e=2e(x-1),即2ex-y-e=0.
(2)∵任意x∈R,f(x)>m恒成立,
∴只要f(x)min>m即可,
令f′(x)>0⇒x>-1,即函数f(x)的单调递增区间是(-1,+∞);
由f′(x)<0⇒x<-1,即函数f(x)的单调递减区间是(-∞,-1);
∴当x=-1时,f(x)min=f(-1)=0,
∴实数m的取值范围(-∞,0).
点评:本题主要考查了实际问题中导数的意义,以及利用导数研究函数的单调性等基础知识,考查恒成立问题的等价转化能力及计算能力,属于中档题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
从4部甲型和5部乙型手机中任意取出3部,其中至少要有甲型与乙型手机各1部,则不同的取法共有( )
| A、35种 | B、70种 |
| C、84种 | D、140种 |
 如图,△ABC的三个内角分别为A,B,C,cosA=
如图,△ABC的三个内角分别为A,B,C,cosA= 如图,点A是单位圆与x轴正半轴的交点,点B(-
如图,点A是单位圆与x轴正半轴的交点,点B(-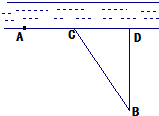 甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的B处,乙厂到河岸的垂足D与A相距50千米,两厂要在此岸边AD之间合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元,若CD=x千米,设总的水管费用为y元,如图所示,
甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的B处,乙厂到河岸的垂足D与A相距50千米,两厂要在此岸边AD之间合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元,若CD=x千米,设总的水管费用为y元,如图所示,