题目内容

在△ABC中，AD是BC边上的高，给出下列结论：①
AD
•（
AB
-
AC
）=0；②|
AB
+
AC
|≥2|
AD
|；③
AC
•
AD
|
AD
|
=|
AB
|sinB．其中结论正确的个数是（　　）
A、0B、1C、2D、3
考点：平面向量数量积的运算
专题：平面向量及应用
分析：①利用向量垂直与数量积的关系即可判断出；
②利用向量的平行四边形法则、中线长和高的关系即可得出；
③利用数量积的定义、直角三角形的边角关系即可得出．
解答： 解：①∵AD是BC边上的高，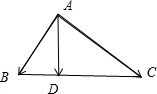
∴
AD
•（
AB
-
AC
）=
AD
•
CB
=0，因此正确；
②取线段BC的中点M，则
AB
+
AC
=2
AM
，|
AM
|≥|
AD
|．
∴|
AB
+
AC
|=2|
AM
|≥|
AD
|，因此正确；
③
AC
•
AD
|
AD
|
=
|
AC
| |
AD
|cos∠DAC
|
AD
|
=|
AD
|=|
AB
|sin∠B．因此正确．
综上可知：①②③正确．
故选：D．
点评：本题考查了向量垂直与数量积的关系、向量的平行四边形法则、中线长和高的关系、数量积的定义、直角三角形的边角关系等基础知识与基本技能方法，考查了推理能力，属于中档题．
练习册系列答案
相关题目
设二次函数f（x）=ax2+（2b+1）x-a-2（a，b∈R，a≠0）在[3，4]上至少有一个零点，则a2+b2的最小值是（　　）
A、1
B、2
C、10
D、
1
100
6个人站成一排，其中甲、乙必须站在两端，且丙、丁相邻，则不同站法的种数为（　　）
A、12B、18C、24D、36
已知a是实数，若（1+i）（3-ai）是纯虚数，则a=（　　）
A、-1B、1C、-3D、3
已知扇形的圆心角为
π
3
，它的半径r=3，则该扇形的面积为（　　）
A、3π
B、
9
2
π
C、
3
2
π
D、
2
3
π
已知抛物线C：y=
1
8
x2，则以抛物线的焦点F为一个焦点，且离心率为
2
的双曲线E的标准方程为（　　）
A、
x2
2
-
y2
2
=1
B、
y2
2
-
x2
2
=1
C、
y2
1
2
-
x2
1
2
=1
D、
x2
1
2
-
y2
1
2
=1
若函数f（x）为偶函数，且
∫
3
0
f（x）dx=8，则
∫
3
-3
[f（x）+2]dx=（　　）
A、12B、16C、20D、28
已知函数f（x）=xex（e为自然对数的底数）
（1）求函数在x=1处的切线方程；  
（2）若任意x∈R，f（x）＞m恒成立，求实数m的取值范围．
求下列函数的导数．
（1）y=2xsin（2x-5）
（2）f（x）=ln
x2+1

（3）y=
2x
x2+1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网