题目内容
已知角α的顶点在原点,始边与x轴的正半轴重合,终边经过点P(-1,
).
=(
,cosx),
=(f(x),cos(x+α)).
(Ⅰ)求sin2α-tanα的值;
(Ⅱ)当
⊥
时,求函数f(x)的最小正周期;
(Ⅲ)在(Ⅱ)的条件下,设△ABC的内角A,B,C的对边分别为a,b,c,若B为锐角,且f(B)=
,b=1,c=
,求a.
| 3 |
| m |
| 1 |
| 2 |
| n |
(Ⅰ)求sin2α-tanα的值;
(Ⅱ)当
| m |
| n |
(Ⅲ)在(Ⅱ)的条件下,设△ABC的内角A,B,C的对边分别为a,b,c,若B为锐角,且f(B)=
| 3 |
| 2 |
| 3 |
考点:余弦定理,数量积判断两个平面向量的垂直关系,两角和与差的正弦函数
专题:三角函数的图像与性质
分析:(Ⅰ)根据三角函数的定义和题意,分别求出sinα、cosα和tanα的值,再代入式子求值;
(Ⅱ)由向量垂直的坐标条件列出方程,求出f(x)再利用二倍角公式、两角和的正弦函数公式化简,再由周期公式求出函数的周期;
(Ⅲ)把f(B)=
代入解析式化简求出角B,由余弦定理和题意列出关于a的方程求解即可.
(Ⅱ)由向量垂直的坐标条件列出方程,求出f(x)再利用二倍角公式、两角和的正弦函数公式化简,再由周期公式求出函数的周期;
(Ⅲ)把f(B)=
| 3 |
| 2 |
解答:
解:(Ⅰ)因为角α终边经过点P(-1,
),则|OP|=2,
所以sinα=
,cosα=-
,tanα=-
,
则sin2α-tanα=2sinαcosα-tanα=-
+
=
----(3分)
(Ⅱ)由
⊥
得,
f(x)+cosxcos(x+α)=0----(4分)
所以
-5 分
=cos2x+
sinxcosx=
(1+cos2x)+
sin2x=sin(2x+
)+
--(7分)
所以f(x)的最小正周期为π--------8 分
(Ⅲ)由f(B)=
得,sin(2B+
)+
=
,
即sin(2B+
)=1,则2B+
=
+2kπ(k∈Z),解得B=
--9 分
由余弦定理得b2=a2+c2-2accosB-----10 分
即 12=a2+
2-2
acos
,
解得,a=1或2---12 分
| 3 |
所以sinα=
| ||
| 2 |
| 1 |
| 2 |
| 3 |
则sin2α-tanα=2sinαcosα-tanα=-
| ||
| 2 |
| 3 |
| ||
| 2 |
(Ⅱ)由
| m |
| n |
| 1 |
| 2 |
所以
|
=cos2x+
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
| 1 |
| 2 |
所以f(x)的最小正周期为π--------8 分
(Ⅲ)由f(B)=
| 3 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| 3 |
| 2 |
即sin(2B+
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
由余弦定理得b2=a2+c2-2accosB-----10 分
即 12=a2+
| 3 |
| 3 |
| π |
| 6 |
解得,a=1或2---12 分
点评:本题考查了三角函数的定义,二倍角公式、两角和的正弦函数公式,以及余弦定理,正弦函数的周期等,涉及的知识点较多,难度不大,关键是熟练掌握公式并会应用.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
已知cosα=-
,且π<α<
,则tanα=( )
| 5 |
| 13 |
| 3π |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
已知函数f(x)在R上满足f(x)=2f(x-2)-x2+8x-8,则曲线y=f(x)在点(1,f(1))处的切线方程是( )
| A、y=2x-1 |
| B、y=x |
| C、y=3x-2 |
| D、y=-2x+3 |
函数y=4x2+
的单调增区间为( )
| 1 |
| x |
| A、(0,+∞) | ||
B、(
| ||
| C、(-∞,-1) | ||
D、(-∞,-
|
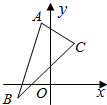 已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).
已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).