题目内容
1.将函数$f(x)=2sin({2x+\frac{π}{4}})$的图象向左平移φ(φ>0)个单位长度后图象关于直线$x=\frac{π}{2}$对称,则φ的最小值为$\frac{π}{8}$.分析 由条件根据函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,求得ω的最小值.
解答 解:将函数$f(x)=2sin({2x+\frac{π}{4}})$的图象向左平移φ(φ>0)个单位长度后,得到函数y=2sin[2(x+φ)+$\frac{π}{4}$]=2sin(2x+2φ+$\frac{π}{4}$)的图象.
再根据得到的图象关于直线x=$\frac{π}{2}$对称,可得2•$\frac{π}{2}$+2φ+$\frac{π}{4}$=kπ+$\frac{π}{2}$,
即解得:φ=$\frac{kπ}{2}$-$\frac{3π}{8}$,k∈z,φ>0,
则ω的最小值为$\frac{π}{8}$.
故答案为:$\frac{π}{8}$.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.

练习册系列答案
相关题目
10.已知点P是抛物线y2=2x上的一个动点,则点P到点D$(2,\frac{3}{2}\sqrt{3})$的距离与点P到y轴的距离之和的最小值为( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |
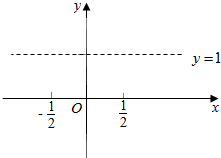 已知直线y=1与曲线y=x2-|x|+a有四个交点.
已知直线y=1与曲线y=x2-|x|+a有四个交点.