题目内容
19.若α为第一象限角,且cosα=$\frac{2}{3}$,则tanα=$\frac{\sqrt{5}}{2}$.分析 由条件利用同角三角函数的基本关系,求得sinα,则tanα的值可求.
解答 解:∵cosα=$\frac{2}{3}$,且α为第一象限角,
∴sinα=$\sqrt{1-co{s}^{2}α}=\sqrt{1-(\frac{2}{3})^{2}}=\frac{\sqrt{5}}{3}$,
∴tanα=$\frac{sinα}{cosα}=\frac{\frac{\sqrt{5}}{3}}{\frac{2}{3}}=\frac{\sqrt{5}}{2}$.
故答案为:$\frac{\sqrt{5}}{2}$.
点评 本题主要考查同角三角函数的基本关系、三角函数在各个象限中的符号,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.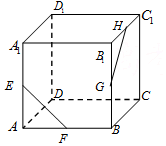 如图所示,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点.则异面直线EF与GH所成的角等于( )
如图所示,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点.则异面直线EF与GH所成的角等于( )
 如图所示,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点.则异面直线EF与GH所成的角等于( )
如图所示,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点.则异面直线EF与GH所成的角等于( )| A. | 120° | B. | 90° | C. | 60° | D. | 45° |
10.过抛物线y=ax2(a>0)的焦点F作一直线交抛物线于P,Q两点,若线段PF和线段FQ的长分别是p,q,则$\frac{1}{p}+\frac{1}{q}$等于( )
| A. | $\frac{1}{4a}$ | B. | $\frac{1}{2a}$ | C. | 2a | D. | 4a |
14.已知函数f(x)对任意的x,y∈R都有f(x+y)=f(x)+f(y),且f(2)=4,则f(1)=( )
| A. | -2 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
4.已知条件p:x<1,条件q:x2-x<0,则p是q成立的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
8.已知实数集R,集合A={x|1<x<3},集合B={x|y=$\frac{1}{\sqrt{x-2}}$},则A∩(∁RB)=( )
| A. | {x|1<x≤2} | B. | {x|1<x<3} | C. | {x|2≤x<3} | D. | {x|1<x<2} |



