题目内容

7．已知a，b，c为直角三角形中的三边长，c为斜边长，若点M（m，n）在直线l：ax+by+3c=0上，则m2+n2的最小值为（　　）
A．2B．3C．4D．9

分析 运用直角三角形的勾股定理，又m2+n2=（$\sqrt{{m}^{2}+{n}^{2}}$）2表示原点到（m，n）的距离的平方，原点到直线l的距离即为所求最小值，运用点到直线的距离，即可得到所求值．

解答 解：a，b，c为直角三角形中的三边长，c为斜边长，
可得a2+b2=c2，
点M（m，n）在直线l：ax+by+3c=0上，
又m2+n2=（$\sqrt{{m}^{2}+{n}^{2}}$）2表示原点到（m，n）的距离的平方，
原点到直线l的距离即为所求最小值，
可得最小值为$\frac{|0+0+3c|}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{3c}{c}$=3．
则m2+n2的最小值为9．
故选：D．

点评 本题考查最值的求法，注意运用点到直线的距离公式，同时考查勾股定理的运用，考查运算能力，属于中档题．

练习册系列答案
相关题目
17．下列关系正确的是（　　）
A．{1}∈{1，2，3}B．{1}?{1，2，3}C．{1}?{1，2，3}D．{1}={1，2，3}
18．（Ⅰ） 在圆x2+y2=4上任取一点P，过点P作x轴的垂线段，D为垂足，当P在圆上运动时，求线段PD的中点Q的轨迹方程；
（Ⅱ）记（Ⅰ）中的轨迹为曲线为C，斜率为k（k≠0）的直线l交曲线C于M（x1，y1），N（x2，y2）两点，记直线OM，ON的斜率分别为k1，k2，当3（k1+k2）=8k时，证明：直线l过定点．
15．设0＜x＜1，a，b都为大于零的常数，则$\frac{{a}^{2}}{x}$+$\frac{{b}^{2}}{1-x}$的最小值为（　　）
A．（a-b）2B．（a+b）2C．a2b2D．a2
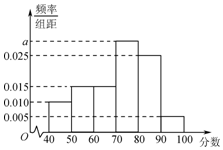2．某校从高一年级学生中随机抽取100名学生，将他们期中考试的数学成绩（均为整数）分成六段：[40，50），[50，60），…，[90，100]后得到频率分布直方图（如图所示），
（1）求分数在[70，80）中的人数；
（2）若用分层抽样的方法从分数在[40，50）和[50，60）的学生中共抽取5 人，该5 人中成绩在[40，50）的有几人；
（3）在（2）中抽取的5人中，随机抽取2 人，求分数在[40，50）和[50，60）各1 人的概率．
12．log36-log32=（　　）
A．1B．2C．3D．4
19．若α为第一象限角，且cosα=$\frac{2}{3}$，则tanα=$\frac{\sqrt{5}}{2}$．
16．定义平面向量的一种运算：$\overrightarrow{a}$?$\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|sin$＜\overrightarrow{a}，\overrightarrow{b}$＞，给出下列命题：
①$\overrightarrow{a}$?$\overrightarrow{b}$=$\overrightarrow{b}$?$\overrightarrow{a}$；
②λ（$\overrightarrow{a}$?$\overrightarrow{b}$）=（$λ\overrightarrow{a}$）?$\overrightarrow{b}$；
③（$\overrightarrow{a}+\overrightarrow{b}$）?$\overrightarrow{c}$=（$\overrightarrow{a}$?$\overrightarrow{c}$）+（$\overrightarrow{b}$?$\overrightarrow{c}$）；
④若$\overrightarrow{a}$=（x1，y1），$\overrightarrow{b}$=（x2，y2）；则$\overrightarrow{a}$?$\overrightarrow{b}$=|x1y2-x2y1|．
其中所有不正确命题的序号是①④．
17．已知函数f（x）=$\left\{\begin{array}{l}-2{x^2}-4x+1，\;\;x≤0\\ x+1，\;\;\;\;\;\;\;\;\;\;\;\;\;\;x＞0.\end{array}\right.$
（1）计算f（f（${log_2}\frac{1}{4}$））的值；
（2）讨论函数f（x）的单调性，并写出f（x）的单调区间；
（3）设函数g（x）=f（x）+c，若函数g（x）有三个零点，求实数c的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网