题目内容
如图,在三棱柱ABC-A′B′C′中,点E,F,H,K分别为AC′,CB′,A′B,B′C′的中点,G为△ABC的重心.从K,H,G,B′中取一点作为P,使得该棱柱恰有2条棱与平面PEF平行,则P为( )
A.K B.H
C.G D.B′
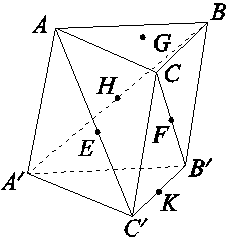
C 解题思路:假如平面PEF与侧棱BB′平行,则和三条侧棱都平行,不满足题意,而FK∥BB′,排除A.假如P为点B′,则平面PEF即平面A′B′C,此平面只与一条棱AB平行,排除D;若P为点H,则HF为△BA′C′的中位线,∴ HF∥A′C′;EF为△ABC′的中位线,∴ EF∥AB,HE为△AB′C′的中位线,∴ HE∥B′C′,显然不合题意,排除B.若P为点G,EF∥AB,则EF∥A′B′,满足条件,故C正确.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目

 -x
-x +1>0”;
+1>0”; ”的既不充分也不必要条件.
”的既不充分也不必要条件. D.
D. 

 ,则O,P两点之间的距离为( )
,则O,P两点之间的距离为( ) B.
B.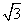 C.1.5 D.2
C.1.5 D.2
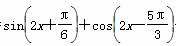 +sin 2x,x∈[0,π].
+sin 2x,x∈[0,π].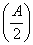 =
=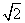 ,a=2,b=
,a=2,b=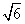 ,求角C.
,求角C.