题目内容
已知f(x)=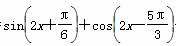 +sin 2x,x∈[0,π].
+sin 2x,x∈[0,π].
(1)求函数f(x)的最小正周期和单调区间;
(2)若△ABC中,f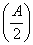 =
=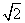 ,a=2,b=
,a=2,b=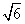 ,求角C.
,求角C.
解析:(1)因为f(x)=sin +cos
+cos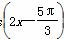 +sin 2x=sin 2x·cos
+sin 2x=sin 2x·cos  +cos 2x·sin
+cos 2x·sin  +cos 2x·cos
+cos 2x·cos  +sin 2x·sin
+sin 2x·sin  +sin 2x=
+sin 2x=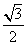 sin 2x+
sin 2x+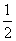 cos 2x+
cos 2x+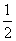 cos 2x-
cos 2x-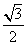 sin 2x+sin 2x=sin 2x+cos 2x=
sin 2x+sin 2x=sin 2x+cos 2x=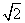 sin
sin .
.
所以f(x)的最小正周期T=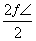 =π.
=π.
因为x∈[0,π],所以2x+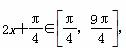 ,
,
当2x+ 时,函数f(x)为单调递增函数;
时,函数f(x)为单调递增函数;
当2x+ 时,函数f(x)为单调递减函数;
时,函数f(x)为单调递减函数;
当2x+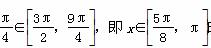 时,函数f(x)为单调递增函数.
时,函数f(x)为单调递增函数.
所以函数f(x)的单调递增区间为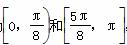 ,单调递减区间为
,单调递减区间为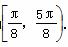 .
.
(2)因为△ABC中,f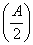 =
=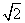 ,所以
,所以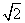 sin
sin =
=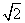 ,所以sin
,所以sin =1,
=1,
因为0<A<π,所以A= ,
,
又因为a=2,b=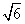 ,所以由正弦定理
,所以由正弦定理 =
=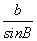 ,得
,得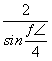 =
= ,
,
所以sin B=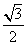 ,即B=
,即B=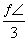 或B=
或B= ,
,
所以C=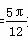 或C=
或C=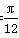 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,B={y|y=x2},则A∩B等于______.
,B={y|y=x2},则A∩B等于______.
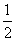 的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=nλ·bn+1(λ为常数,且λ≠1).
的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=nλ·bn+1(λ为常数,且λ≠1).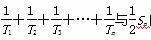 的大小.
的大小.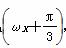 (x∈R,ω>0)的部分图象如图所示,点P是图象的最高点,Q是图象的最低点,且|PQ|=
(x∈R,ω>0)的部分图象如图所示,点P是图象的最高点,Q是图象的最低点,且|PQ|=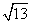 ,则f(x)的最小正周期是( )
,则f(x)的最小正周期是( )

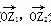 分别对应复数z1,z2,且z1=
分别对应复数z1,z2,且z1=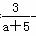 +(10-a2)i,z2=
+(10-a2)i,z2=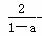 +(2a-5)i(a∈R),若
+(2a-5)i(a∈R),若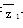 +z2是实数.
+z2是实数.