题目内容
从点P出发的三条射线PA，PB，PC两两成60°角，且分别与球O相切于A，B，C三点，若球的体积为
，则O，P两点之间的距离为( )
A.
B.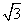
C．1.5 D．2
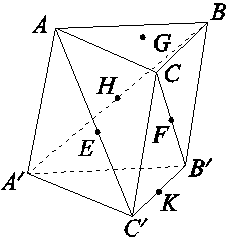
B 解题思路：构造法解决，点P看作是一个正方体的一个顶点，三条射线看作以P为起点的三条面对角线，球O与这三条面对角线相切于A，B，C三点，根据球和正方体的对称可知，球O的球心O为正方体的中心(体对角线的中点)．由球的体积得到球半径为1，那么构造的正方体边长等于球体的直径，即为2，所以OP长度为此正方体体对角线的一半，即为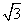，故选B.
练习册系列答案
相关题目
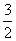a2 B.
a2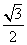
a2 D.
a2
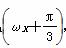(x∈R，ω＞0)的部分图象如图所示，点P是图象的最高点，Q是图象的最低点，且|PQ|＝
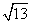，则f(x)的最小正周期是( )