题目内容
在各项均为正数的等比数列{an}中，已知a3＋a4＝11a2a4，且它的前2n项的和等于它的前2n项中偶数项之和的11倍，则数列{an}的通项公式an＝________.
命题立意：本题考查等比数列的通项公式及其前n项和公式等知识，考查考生的运算运力．
解题思路：设等比数列{an}的公比为q，前2n项和为S2n，前2n项中偶数项之和为Tn，由题意知q≠1，则S2n＝
，Tn＝
.由题意可知S2n＝11Tn，即＝
.解得q＝
(或令n＝1，则S2＝11T1，即a1＋a2＝11a2，化简得a1＝10a2，故q＝)．又a3＋a4＝11a2a4，所以a1q2＋a1q3＝11a
q4，化简得1＋q＝11a1q2，将q＝代入可得a1＝10，故an＝a1qn－1＝
＝102－n.
练习册系列答案
相关题目
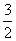a2 B.
a2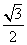
a2 D.
a2
的等比数列，且1－a2是a1与1＋a3的等比中项，前n项和为Sn；数列{bn}是等差数列，b1＝8，其前n项和Tn满足Tn＝nλ·bn＋1(λ为常数，且λ≠1)．
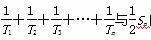的大小．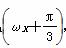
(x∈R，ω＞0)的部分图象如图所示，点P是图象的最高点，Q是图象的最低点，且|PQ|＝
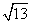，则f(x)的最小正周期是( )