题目内容
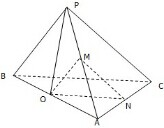已知三棱锥P-ABC中，PA=PB=PC，BC⊥AC，M为PA中点，P在面ABC上的射影为O，O在AC上的射影为N，求证：平面OMN∥平面PBC．考点：平面与平面平行的判定
专题：空间位置关系与距离
分析：由已知得O是AB中点，N是AC中点，从而ON∥BC，MO∥PB，MN∥PC，由此能证明平面OMN∥平面PBC．
解答：
证明：∵三棱锥P-ABC中，PA=PB=PC，BC⊥AC，M为PA中点，
P在面ABC上的射影为O，O在AC上的射影为N，
∴O是AB中点，N是AC中点，
∴ON∥BC，MO∥PB，MN∥PC，
∵OM∩MN=M，OM、MN?平面OMN，
∴平面OMN∥平面PBC．
P在面ABC上的射影为O，O在AC上的射影为N，
∴O是AB中点，N是AC中点，
∴ON∥BC，MO∥PB，MN∥PC，
∵OM∩MN=M，OM、MN?平面OMN，
∴平面OMN∥平面PBC．
点评：本题考查平面与平面平行的证明，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
直线l交椭圆
+
=1于A，B两点，若AB的中点为M=（2，1），则l的方程为（ ）
| x2 |
| 16 |
| y2 |
| 12 |
| A、2x-3y-1=0 |
| B、3x-2y-4=0 |
| C、2x+3y-7=0 |
| D、3x+2y-8=0 |
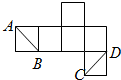
如图是正方体的平面展开图，则在这个正方体中AB与CD的位置关系为（ ）
| A、平行 |
| B、相交成60°角 |
| C、异面且垂直 |
| D、异面且成60°角 |
当实数x，y满足
时，1≤ax+y≤4恒成立，则实数a的取值范围是（ ）
|
A、[-
| ||||
B、[-
| ||||
C、[1，
| ||||
D、[
|