题目内容
在平面直角坐标系中,定义点P(x1,y1)、Q(x2,y2)之间的直角距离为L(P,Q)=|x1-x2|+|y1-y2|,点A(x,1),B(1,2),C(5,2)
(1)若L(A,B)>L(A,C),求x的取值范围;
(2)当x∈R时,不等式L(A,B)≤t+L(A,C)恒成立,求t的最小值.
(1)若L(A,B)>L(A,C),求x的取值范围;
(2)当x∈R时,不等式L(A,B)≤t+L(A,C)恒成立,求t的最小值.
考点:进行简单的合情推理
专题:新定义,不等式的解法及应用,推理和证明
分析:(1)根据定义写出L(A,B),L(A,C)的表达式,最后通过解不等式求出x的取值范围;
(2)当x∈R时,不等式L(A,B)≤t+L(A,C)恒成立即当x∈R时,不等式|x-1|≤|x-5|+t恒成立,
运用分离变量,即有t≥|x-1|-|x-5|恒成立,可用去绝对值的方法或绝对值不等式的性质,求得右边的最大值为4,令t不小于4即可.
(2)当x∈R时,不等式L(A,B)≤t+L(A,C)恒成立即当x∈R时,不等式|x-1|≤|x-5|+t恒成立,
运用分离变量,即有t≥|x-1|-|x-5|恒成立,可用去绝对值的方法或绝对值不等式的性质,求得右边的最大值为4,令t不小于4即可.
解答:
解:(1)由定义得|x-1|+1>|x-5|+1,
即|x-1|>|x-5|,两边平方得8x>24,
解得x>3,
(2)当x∈R时,不等式|x-1|≤|x-5|+t恒成立,
也就是t≥|x-1|-|x-5|恒成立,
法一:令函数f(x)=|x-1|-|x-5|=
,
所以f(x)max=4,
要使原不等式恒成立只要t≥4即可,
故tmin=4.
法二:运用绝对值不等式性质.
因为|x-1|-|x-5|≤|(x-1)-(x-5)|=4,所以t≥4,tmin=4.
故t的最小值为:4.
即|x-1|>|x-5|,两边平方得8x>24,
解得x>3,
(2)当x∈R时,不等式|x-1|≤|x-5|+t恒成立,
也就是t≥|x-1|-|x-5|恒成立,
法一:令函数f(x)=|x-1|-|x-5|=
|
所以f(x)max=4,
要使原不等式恒成立只要t≥4即可,
故tmin=4.
法二:运用绝对值不等式性质.
因为|x-1|-|x-5|≤|(x-1)-(x-5)|=4,所以t≥4,tmin=4.
故t的最小值为:4.
点评:本题考查新定义:直角距离的理解和运用,考查绝对值不等式的解法,以及不等式恒成立问题,转化为求函数的最值,属于中档题.

练习册系列答案
相关题目
已知双曲线一焦点坐标为(0,-5),一渐近线方程为3x+4y=0,则双曲线的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
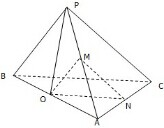 已知三棱锥P-ABC中,PA=PB=PC,BC⊥AC,M为PA中点,P在面ABC上的射影为O,O在AC上的射影为N,求证:平面OMN∥平面PBC.
已知三棱锥P-ABC中,PA=PB=PC,BC⊥AC,M为PA中点,P在面ABC上的射影为O,O在AC上的射影为N,求证:平面OMN∥平面PBC.