题目内容
已知函数f(x)=mx3+nx+k为奇函数,且f(x)在x=
时取得极值-
.
(Ⅰ)求实数m,n,k的值;
(Ⅱ)过定点Q(a,b)(a>0)作曲线y=f(x)的切线,若这样的切线可以作出三条.求证:-a<b<f(a).
| ||
| 3 |
2
| ||
| 9 |
(Ⅰ)求实数m,n,k的值;
(Ⅱ)过定点Q(a,b)(a>0)作曲线y=f(x)的切线,若这样的切线可以作出三条.求证:-a<b<f(a).
考点:利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)根据奇函数的性质,得到f(0)=0,求出k,在根据f(x)在x=
时取得极值-
得到f′(
)=0,f(
)=-
,代入求值即可.
(Ⅱ)先设切点为(t,t3-t),根据导数的几何是切线的斜率,列出关于t的一个方程,然后根据此方程必须有三个不同的实数解,结合相应函数有三个不同的零点,最后利用函数的极值点列出不等关系即可证明.
| ||
| 3 |
2
| ||
| 9 |
| ||
| 3 |
| ||
| 3 |
2
| ||
| 9 |
(Ⅱ)先设切点为(t,t3-t),根据导数的几何是切线的斜率,列出关于t的一个方程,然后根据此方程必须有三个不同的实数解,结合相应函数有三个不同的零点,最后利用函数的极值点列出不等关系即可证明.
解答:
解(Ⅰ):∵f(x)=mx3+nx+k为奇函数.
∴f(0)=0,
∴k=0,
∴f′(x)=3mx3+n,
∵f(x)在x=
时取得极值-
.
∴f′(
)=0,f(
)=-
∴
解得m=1,n=-1,
(Ⅱ)设切点P(t,t3-t),则切线方程为:y-t3+t=(3t2-1)(x-t),
∵过定点Q(a,b),
∴b-t3+t=(3t2-1)(a-t),
即2t3-3at2+a+b=0,
∵直线PQ有三条,
∴方程2t3-3at2+a+b=0有三个不同的实数解,(8分)
∴函数g(t)=2t3-3at2+a+b有三个不同的零点,
∴g′(t)=6t2-6at,
令g′(t)=0,解得t=0,或t=a,
当t=0时,g(t)有极大值,极大值为g(0)=a+b,
当t=a时,g(t)有极小值,极小值为g(a)=a-a3+b,
∴
∴-a<b<a3-a,
∴-a<b<f(a).
∴f(0)=0,
∴k=0,
∴f′(x)=3mx3+n,
∵f(x)在x=
| ||
| 3 |
2
| ||
| 9 |
∴f′(
| ||
| 3 |
| ||
| 3 |
2
| ||
| 9 |
∴
|
解得m=1,n=-1,
(Ⅱ)设切点P(t,t3-t),则切线方程为:y-t3+t=(3t2-1)(x-t),
∵过定点Q(a,b),
∴b-t3+t=(3t2-1)(a-t),
即2t3-3at2+a+b=0,
∵直线PQ有三条,
∴方程2t3-3at2+a+b=0有三个不同的实数解,(8分)
∴函数g(t)=2t3-3at2+a+b有三个不同的零点,
∴g′(t)=6t2-6at,
令g′(t)=0,解得t=0,或t=a,
当t=0时,g(t)有极大值,极大值为g(0)=a+b,
当t=a时,g(t)有极小值,极小值为g(a)=a-a3+b,
∴
|
∴-a<b<a3-a,
∴-a<b<f(a).
点评:本小题主要考查利用导数研究曲线上某点切线方程、利用导数研究函数的极值、函数的零点、直线的方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
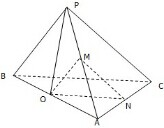 已知三棱锥P-ABC中,PA=PB=PC,BC⊥AC,M为PA中点,P在面ABC上的射影为O,O在AC上的射影为N,求证:平面OMN∥平面PBC.
已知三棱锥P-ABC中,PA=PB=PC,BC⊥AC,M为PA中点,P在面ABC上的射影为O,O在AC上的射影为N,求证:平面OMN∥平面PBC.