题目内容
直线l交椭圆
+
=1于A,B两点,若AB的中点为M=(2,1),则l的方程为( )
| x2 |
| 16 |
| y2 |
| 12 |
| A、2x-3y-1=0 |
| B、3x-2y-4=0 |
| C、2x+3y-7=0 |
| D、3x+2y-8=0 |
考点:直线与圆锥曲线的关系
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:设A(x1,y1),B(x2,y2),两点在椭圆上,可得3x12+4y12=48,3x22+4y22=48.两式相减,再利用直线l的斜率,中点坐标公式,即可得出.
解答:
解:设A(x1,y1),B(x2,y2),
∵M(2,1)是线段AB的中点,
∴x1+x2=4,y1+y2=2,
∵此两点在椭圆上,∴3x12+4y12=48,3x22+4y22=48.
∴,3(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0,
∴k=
=-
=-
.
∴直线l的方程为y-1=-
(x-2),化为3x+2y-8=0.
故选D.
∵M(2,1)是线段AB的中点,
∴x1+x2=4,y1+y2=2,
∵此两点在椭圆上,∴3x12+4y12=48,3x22+4y22=48.
∴,3(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0,
∴k=
| y1-y2 |
| x1-x2 |
| 3×4 |
| 4×2 |
| 3 |
| 2 |
∴直线l的方程为y-1=-
| 3 |
| 2 |
故选D.
点评:本题考查直线与椭圆的综合,考查弦中点问题,正确运用点差法解决中点弦问题是解题的关键,属于中档题.

练习册系列答案
相关题目
 如图,在平面直角坐标系xoy中,椭圆
如图,在平面直角坐标系xoy中,椭圆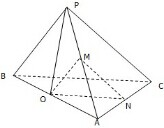 已知三棱锥P-ABC中,PA=PB=PC,BC⊥AC,M为PA中点,P在面ABC上的射影为O,O在AC上的射影为N,求证:平面OMN∥平面PBC.
已知三棱锥P-ABC中,PA=PB=PC,BC⊥AC,M为PA中点,P在面ABC上的射影为O,O在AC上的射影为N,求证:平面OMN∥平面PBC.